The set of values of $x$ satisfying $∣ ∣ {sin}^{- 1} x ∣ ∣ < ∣ ∣ {cos}^{- 1} x ∣ ∣,$ is

A

$[- 1, 1 / \sqrt{2})$

B

$[- 1, 1 / \sqrt{2}] \cup [1 / \sqrt{2}, 1]$

C

$(- 1, 1 / \sqrt{2})$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

We know that $0 \leq {cos}^{- 1} x \leq π$
$∴ ∣ ∣ {cos}^{- 1} x ∣ ∣ = {cos}^{- 1} x$

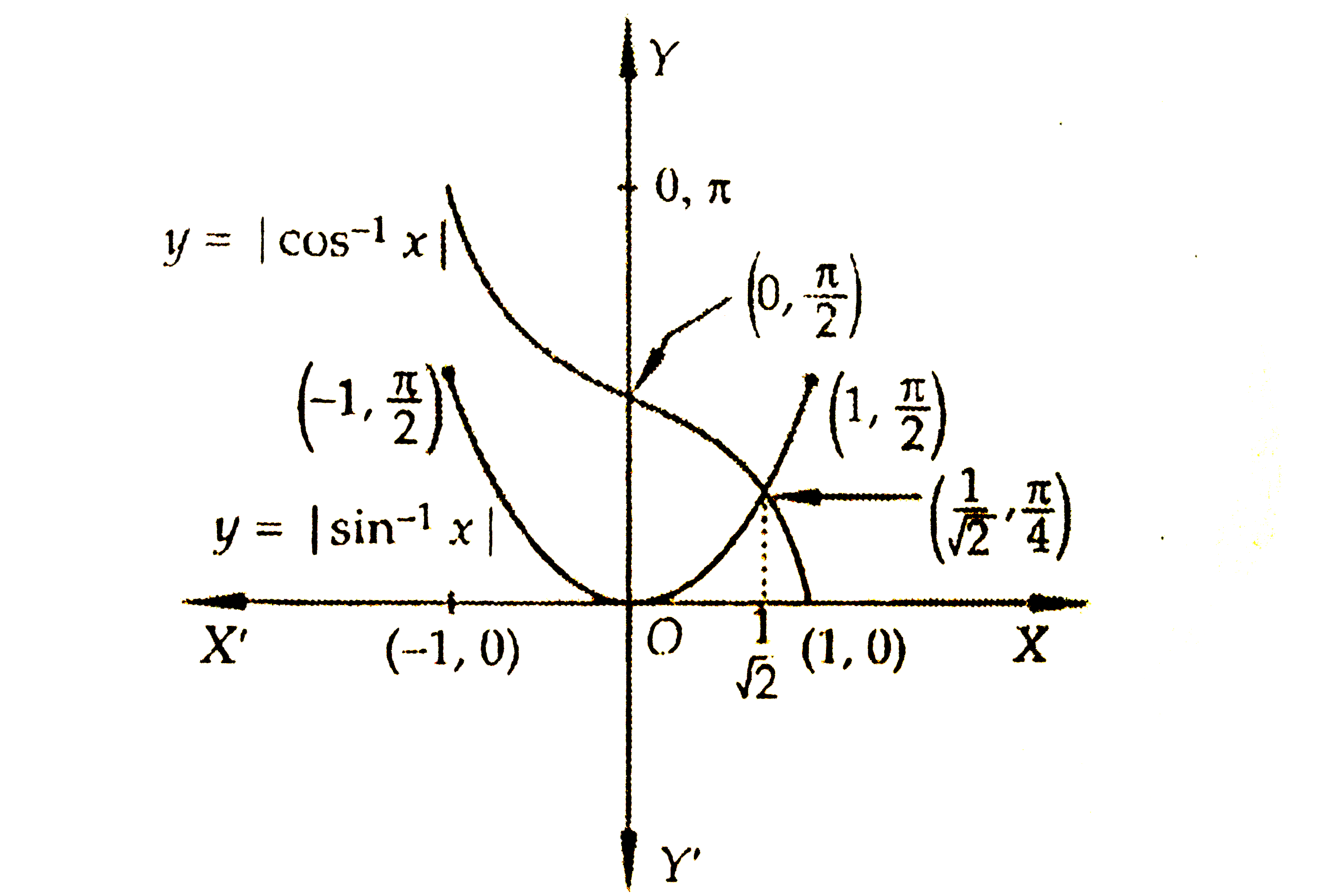
It is evident from the graphs of $y = ∣ ∣ {sin}^{- 1} x ∣ ∣ and y = ∣ ∣ {cos}^{- 1} x ∣ ∣$ that
$∣ ∣ {sin}^{- 1} x ∣ ∣ {cos}^{- 1} x ∣ f or a l l x \in [- 1, 1 / \sqrt{2}$

Updated on:21/07/2023

|

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The set of values of x satisfying $2 \leq | x - 3 | < 4$ is
A $(- 1, 1] \cup [5, 7)$
B $- 4 \leq x \leq 2$
C $- 1 < x < 7$ or $x \geq 5$
D $x < 7$ or $x \geq 5$
The set of real values of x satisfying ||x-1|-1| $\leq$ 1 is
A[-1,1]
B[-1,1]
C[-1,3]
D[-2,2]
The set of all real values of x satisfying ${sin}^{- 1} \sqrt{x} < \frac{π}{4}$ , is
A $(0, \frac{1}{2})$
B $[0, \frac{1}{2})$
C $(0, \frac{1}{2}]$
D $[0, \frac{1}{2}]$

OBJECTIVE RD SHARMA-INVERSE TRIGONOMETRIC FUNCTIONS -Section I - Solved Mcqs

Home
Ask Doubt
Profile