Prove that a line joining the midpoints of any two sides of a triangle is parallel to the third side. (Using converse of basic proportionality theorem)Solution in Gujrati
Step by step video & image solution for Prove that a line joining the midpoints of any two sides of a triangle is parallel to the third side. (Using converse of basic proportionality theorem) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILAR TRIANGLES BOOK - NCERT GUJARATICHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.2
13 Videos
- SIMILAR TRIANGLES BOOK - NCERT GUJARATICHAPTER - SIMILAR TRIANGLES EXERCISE - EXERCISE - 8.3
6 Videos
- SIMILAR TRIANGLES BOOK - NCERT GUJARATICHAPTER - SIMILAR TRIANGLES EXERCISE - DO THIS
5 Videos
- SETSBOOK - NCERT GUJARATICHAPTER - SETSEXERCISE - Try This
11 Videos
- STATISTICSBOOK - NCERT GUJARATICHAPTER - STATISTICSEXERCISE - THINK AND DISCUSS
8 Videos
Similar Questions
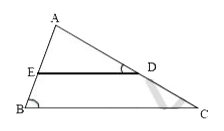
In the given figure, ∠ADE = ∠B
(i) Show that ΔABC ~ ΔADE
(ii) If AD = 3.8 cm, AE = 3.6cm, BE = 2.1 cm and BC = 4.2 cm, find DE.
View SolutionD, E, F are mid points of sides BC, CA, AB of ΔABC. Find the ratio of areas of ΔDEFandΔABC.
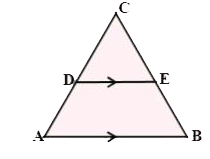
View SolutionWhat value(s) of x will make DE || AB, in the given figure ?
AD = 8x + 9 , CD= x + 3 ,
BE = 3x + 4 , CE = x.
View SolutionWrite some sets of your choice, involving algebraic and geometrical ideas.
View SolutionThe mean value can be calculated from both ungrouped and grouped data. Which one do you think is more accurate? Why?
View SolutionConverse of Basis proportionality theorem : If a line divides any two sides of a triangle in the same ratio; then the line must be parallel to the third side.
View Solutionप्रमेय 2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज कि किन्ही दो भुजाओ के मध्य -बिन्दुओ को मिलाने वाली रेखा तीसरी भुजा के समान्तर होती है (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके है
View Solutionसिद्ध कीजिये की किसी त्रिभुज की दो भुजाओं के मध्य बिन्दुओ को मिलाने वाली रेखा तीसरी भुजा की आधी होती है|
View Solutionसिद्ध कीजिए की एक त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समान्तर होती है।
View SolutionUsing the inverse of the basic proportionality theorem, prove that the line between the midpoints of the two sides is parallel to the third arm.
View SolutionProve that a line drawn through the mid-point of one side of a Triangle parallel to another side bisects the third side (Using Basic proportionality theorem).
View SolutionProve that a line joining the mid points of any two sides of a Triangle is parallel to the third side. (Using Converse of Basis Proportionality theorem)
View SolutionUsing Theorem , prove that the line joining the mid-point of any two sides of a triangle is parallel to the third side. ( Recall that you have done it is class IX) .
View Solutionविश्लेषिक विधि से सिद्ध कीजिए कि किसी त्रिभुज में दो भुजाओं के मध्य - बिंदुओं को मिलाने वाली रेखा तीसरी भुजा की आधी होती है ।
View SolutionProve that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side (Using basic proportionality theorem).
View Solution