If a straight line divdes two sides of a triangle proportionally, then the straight line a parallel to third sides, (Converse of Thales theorem). Prove.Solution in Kannada
The correct Answer is:DE∣∣BC
Step by step video, text & image solution for If a straight line divdes two sides of a triangle proportionally, then the straight line a parallel to third sides, (Converse of Thales theorem). Prove. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - OSWAAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TOPIC-1 BASIC PROPORTIONALITY THEOREM (VERY SHORT ANSWER TYPE QUESTIONS)17videos
TRIANGLES
- BOOK - OSWAAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TOPIC-1 BASIC PROPORTIONALITY THEOREM (LONG ANSWER TYPE QUESTIONS-(II))6videos
TRIANGLES
- BOOK - OSWAAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - TOPIC-1 BASIC PROPORTIONALITY THEOREM (SHORT ANSWER TYPE QUESTIONS)19videos
TRIANGLES
- BOOK - OSWAAL PUBLICATIONCHAPTER - SURFACE AREA AND VOLUMESEXERCISE - EXERCISE 15.55videos
SURFACE AREA AND VOLUMES
Similar Questions
State "Basic proportionality theorem"
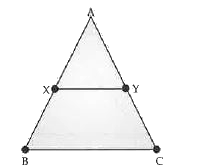
07:22View SolutionIn a ΔABC, XY∣∣BC and XY=12BC. If the area of ΔAXY=10cm2. Find the area of trapezium XYCB.
 04:59View Solution
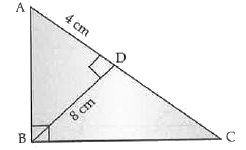
04:59View SolutionIn ΔABC, ∠ABC=90∘, BD⊥AC. If BD=8cm, AD=4cm, find CD .
 02:31View Solution
02:31View SolutionA copper wire, 3mm in diameter , is wound about a cylinder whose length is 12cm, and diameter 10cm, so as to cover the curved surface of the cylinder . Find the length and mass of the wire, assuming the density of copper to be 8.88gpercm3
07:37View SolutionBasic proportionality Theorem or Thales Theorem - If a line is drawn parallel to one side of a triangle intersecting the other two sides; then it divides the two sides in the same ratio.
03:42View SolutionConverse of Basis proportionality theorem : If a line divides any two sides of a triangle in the same ratio; then the line must be parallel to the third side.
01:07View SolutionWith the help of Thales' theorem prove that the line drawn through mid-point of one side of a triangle parallel to another side bisects the third side.
08:47View SolutionProve by the theorem of Thales that the third side of a triangle is parallel to the line segment obtained by joining the mid-points of any two sides of the triangle and is half in length of its third side.
02:24View SolutionProve that a line joining the mid points of any two sides of a Triangle is parallel to the third side. (Using Converse of Basis Proportionality theorem)
02:33View SolutionA straight line drawn ____ to a side of a triangle divides the order two sides proportionality.
02:30View SolutionState and prove Thales theorem
Statement
A straight line drawn parallel to a side of triangle intersecting the other two sides , divides the sides in the same ratio.02:53View SolutionProve that a line joining the midpoints of any two sides of a triangle is parallel to the third side. (Using converse of basic proportionality theorem)
03:52View SolutionProve that a line joining the midpoints of any two sides of a triangle is parallel to the third side. (Using converse of basic proportionality theorem)
02:58View SolutionProve that a line joining the midpoints of any two sides of a triangle is parallel to the third side. (Using converse of basic proportionality theorem)
05:34View Solutionথ্যালাসের বিপরীত উপপাদ্যের সাহায্যে প্রমাণ করো যে, ত্রিভুজের মধ্যবিন্দুরদ্বয়ের সংযোজক সরলরেখাংশ তৃতীয় বাহুর সমান্তরাল ।
06:25View Solution

