Draw a pair of radii OA and OB in a circle such that ∠BOA=120∘. Draw the bisector of ∠BOA and draw lines perpendiculars to OA and OB at A and B. These lines meet on the bisector of ∠BOA at a point which is the external point and the perpendicular lines are the required tangents. Construct and Justify. Solution in Gujrati
Step by step video & image solution for Draw a pair of radii OA and OB in a circle such that /_BOA=120^(@). Draw the bisector of /_BOA and draw lines perpendiculars to OA and OB at A and B. These lines meet on the bisector of /_BOA at a point which is the external point and the perpendicular lines are the required tangents. Construct and Justify. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND SECANTS TO A CIRCLEBook:NCERT GUJARATIChapter:TANGENTS AND SECANTS TO A CIRCLEExercise:Do this
Explore 6 Videos
- STATISTICSBook:NCERT GUJARATIChapter:STATISTICSExercise:THINK AND DISCUSS
Explore 8 Videos
- TRIGONOMETRY Book:NCERT GUJARATIChapter:TRIGONOMETRY Exercise:OPTIONAL EXERCISE
Explore 6 Videos
Similar Questions
Draw a circle with any radius. Draw four tangents at different points. How many more tangets can you draw to this circle ?
View SolutionThe mean value can be calculated from both ungrouped and grouped data. Which one do you think is more accurate? Why?
View SolutionProve that cotθ−cosθcotθ+cosθ=cosecθ−1cosecθ+1
View Solution6.0 सेमी लम्बाई का एक रेखाखण्ड खींचिए और इसके लम्ब समद्विभाजक की रचना कीजिए।
View SolutionOA and OB are two perpendicular straight lines. A straight line AB is drawn in such a manner that OA+OB=8. Find the locus of the mid point of AB.
View SolutionDraw a pair of radii OA and OB such that ∠BOA=120∘ . Draw the bisector of ∠BOA and draw lines perpendiculars to OA and OB at A and B . These lines meet on the bisector of ∠BOA at a point which is the external point and the perpendicular lines are the required tangents . Construct and justify .
View SolutionDraw a perpendicular bisector of line segment AB = 8cm.
View Solution/_BOA=120^(0) Draw the radii of OA and OB, respectively. /_BOA Draw an isosceles line to and draw perpendiculars to OA and OB at A and B. These lines /_BOA Intersect the line of intersection at the outer point. These can be taken as the tangents we want. Build. Justify.
View SolutionDraw a pair of radii OA and OB in a circle such that ∠BOA=120∘. Draw the bisector of ∠BOA and draw lines perpendiculars to OA and OB at A and B. These lines meet on the bisector of ∠BOA at a point which is the external point and the perpendicular lines are the required tangents. Construct and Justify.
View SolutionIn the Fig. given below, OB is the perpendicular bisector of the line segment DE, FA⊥OB and FE intersects OB at the point C. Prove that 1OA+1OB=2OC
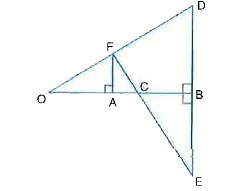
View SolutionIn figure 6.13, OB is the perpendicular bisector of the line segment DE, FA _|_ OB And FE intersects line segment OB at point C. Prove that (1)/(OA)+(1)/(OB)=(2)/(OC) is.
View Solution5.6 सेमी लम्बाई का एक रेखाखंड खींचिए और इसके लंब समद्विभाजक की रचना कीजिए।
View SolutionDraw an angle with vertex O. Consider point A on one of its sides and B on another side such that OA = OB. overset_(OA And overset_(OB Draw the perpendicular bisector of. Suppose they intersect at P. What is PA = PB?
View SolutionDraw a line segment of length 9.5 cm and construct its perpendicular bisector.
View SolutionDraw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB, Draw the perpendicular bisectors of O̅A and O̅B. Let them meet at P. Is PA = PB?
View Solution