OA and OB are two perpendicular straight lines. A straight line AB is drawn in such a manner that OA+OB=8. Find the locus of the mid point of AB.
The correct Answer is:x+y=4
To find the locus of the midpoint of line segment AB, where OA and OB are two perpendicular lines and OA + OB = 8, we can follow these steps:
Step 1: Define the Coordinates
Let the point O be the origin (0, 0). Since OA and OB are perpendicular, we can assume:
- Point A lies on the x-axis, so its coordinates are (a, 0).
- Point B lies on the y-axis, so its coordinates are (0, b).
Step 2: Express the Condition
According to the problem, the sum of OA and OB is given by:
OA+OB=8
This translates to:
a+b=8
Step 3: Find the Midpoint of AB
The midpoint M of line segment AB can be calculated using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
M=(a+02,0+b2)=(a2,b2)
Step 4: Express a and b in terms of x and y
Let the coordinates of the midpoint M be (x, y). Thus, we have:
x=a2andy=b2
From these, we can express a and b as:
a=2xandb=2y
Step 5: Substitute into the Condition
Now substitute a and b into the equation a+b=8:
2x+2y=8
Dividing the entire equation by 2 gives:
x+y=4
Step 6: Conclusion
The locus of the midpoint M of line segment AB is the line given by the equation:
x+y=4
Let the point O be the origin (0, 0). Since OA and OB are perpendicular, we can assume:
- Point A lies on the x-axis, so its coordinates are (a, 0).
- Point B lies on the y-axis, so its coordinates are (0, b).
According to the problem, the sum of OA and OB is given by:
OA+OB=8
This translates to:
a+b=8
The midpoint M of line segment AB can be calculated using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
M=(a+02,0+b2)=(a2,b2)
Let the coordinates of the midpoint M be (x, y). Thus, we have:
x=a2andy=b2
From these, we can express a and b as:
a=2xandb=2y
Now substitute a and b into the equation a+b=8:
2x+2y=8
Dividing the entire equation by 2 gives:
x+y=4
The locus of the midpoint M of line segment AB is the line given by the equation:
x+y=4
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Single Option Correct Type Questions)
15 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (More Than One Correct Option Type Questions)
7 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 3
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
If O be origin and A is a point on the locus y2=8x .find the locus of the middle point of OA
View SolutionA straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
View SolutionA point P is taken on 'L' such that 2OP=1OA+1OB , then the locus of P is
View SolutionA circle passes through a fixed point A and cuts two perpendicular straight lines through A in B and C. If the straight line BC passes through a fixed-point (x1,y1), the locus of the centre of the circle, is
View SolutionA rod of length / slides with its ends on two perpendicular lines. Find the locus of its mid-point.
View SolutionThe straight line xa+yb=1 cuts the axes in A and B and a line perpendicular to AB cuts the axes in P and Q. Find the locus of the point of intersection of AQ and BP .
View SolutionThe graph between the displacement x and time t for a particle moving in a straight line is shown in the figure. During the interval OA,AB,BC and CD the acceleration of the particle is
OA,AB,BC,CD
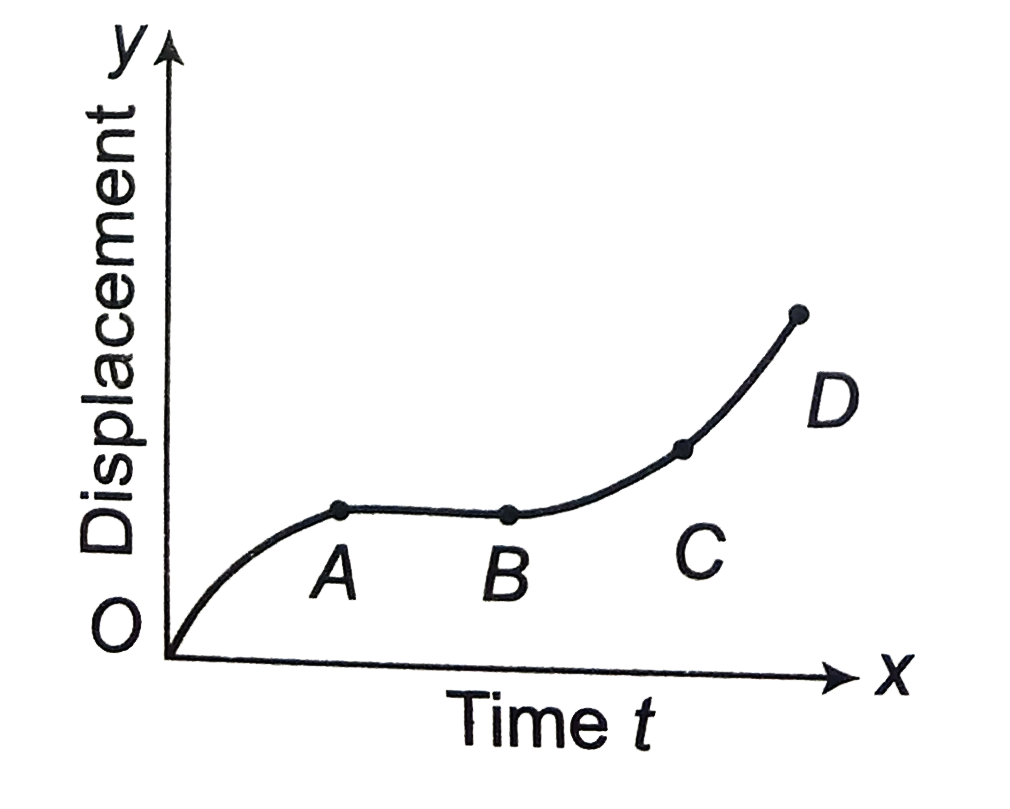
View SolutionTwo mutually perpendicular chords OA and OB are drawn through the vertex 'O' of a parabola y2=4ax. Then find the locus of the circumcentre of triangle OAB.
View SolutionDraw a straight line AB=6.5 cm. draw another line which is parallel to AB at a distance of 2.8 cm from it.
View SolutionA straight lien is drawn from a fixed point O metting a fixed straight line P. A point Q is taken on the line OP such that OP.OQ is constant. Show that the locus of Q is a circle.
View Solution
