Two wires are together end to end . The wires are made of the same material , but the diameter of one is twice that of the other . They are subjected to a tension of 4.60N. The thin wire has a length of 40.0cm and a linear mass density of 2.00g/m. The combination is fixed at both ends and vibrated in such a way that two antinodes are present , with the node between them being precisely at the weld . (a) What is the frequency of vibration ? (b) Find the length of the thick wire .
The mass per volume density , the tension , and the frequency must be the same for the two wires . The linear density , wave speed , wavelength and node - to node distance for it .
a. Since the first node is at the weld , the wavelength in the thin wire is
lmbda=2L=80.0cm
The frequency and tension are the same in both sections , so
f=vλ=12L√Tμ=12(0.400m)√4.60N0.00200kg/m=59.9Hz
b. Since the thick wire is twice the diameter , it will have four times the cross - sectional area , and a linear density μ' that is four times that of the thin wire . μ'=4(2.00g/m)=0.00800kg/m.
L'=λ'2=v'2f=12f√Tμ'
=12(59.9Hz)√4.60N0.00800kg/m=20.0cm
Note that the thick wire is half the length of the thin wire . We could have reasoned the answer by noting that the wave speed on the thick wire is half as large , so the wavelength should be half as large for the same frequency .
Similar Questions
A wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View SolutionA wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
View Solution
Knowledge Check
Two wires of equal length are made of the same material. Wire A has a diameter that is twice as that of wire B. If identical weights are suspended from the ends of these wires, the increase in length is
AFour times for wire A as for wire BBTwice for wire A as for white BCHalf for wire A as for wire BDOne-fourth for wire A as for wire BThe ratio of diameters of two wires of the same material and same length is n : 1. If the same load is applied to both the wires then the increase in the length of the thin wire is (n>1)
An14 timesBn12 timesCn timesDn2 timesThe ratio of diameters of two wires of the same material and same length is n : 1. If the same load is applied to both the wires then the increase in the length of the thin wire is (n>1)
An14 timesBn1/2 timesCn timesDn2 times
The ratio of frequencies of two wires having same length and same tension and made of the same material is 2:3.If the diameter of one wire be 0.09 cm , then determine the diameter of the other.
View SolutionTwo similar sonometer wires of the same material under the same tension produces 3 beats per second. The length of one wire is 40 cm and that of the other is 40.1 cm. Calculate the frequency of the two wires ?
View SolutionA 1m long wire having tension of 100 N and of linear mass density 0.01 kg/m is fixed and A and free at end B. the point C which is 20cm from end B is constrained to be stationary. To create resonance in the wire, the minimum frequency of the tuning fork will be :
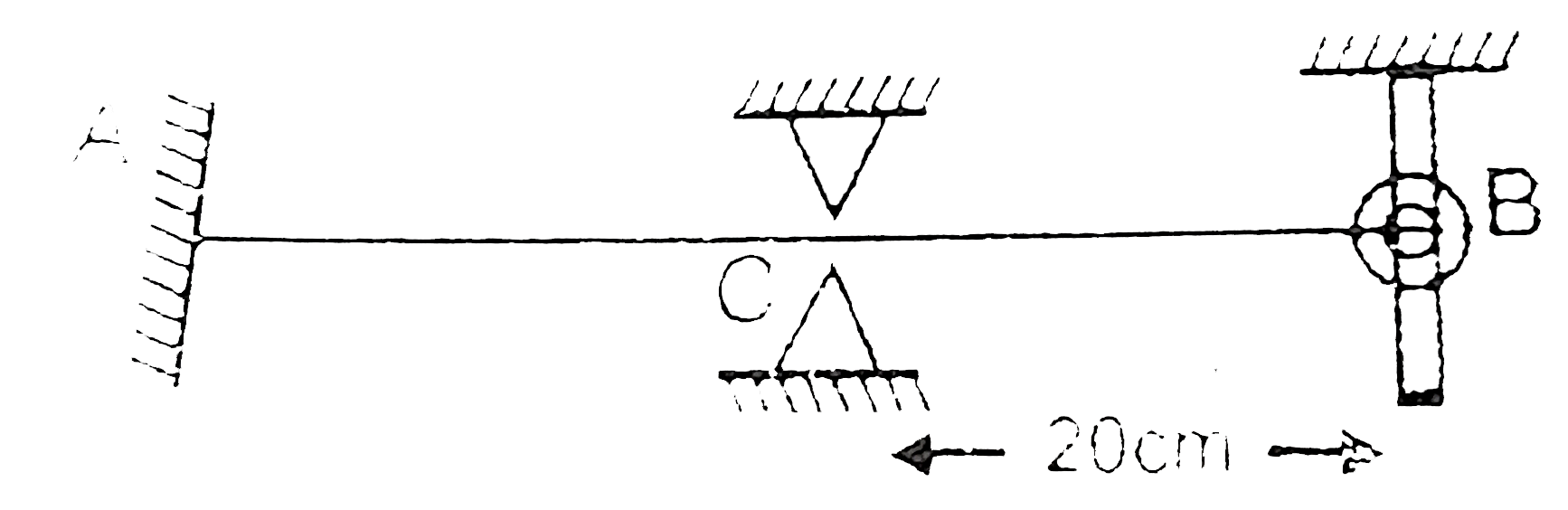
View SolutionA steel wire of mass 4.0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
View SolutionA steel wire of mass 4.0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
View Solution
