The water level in a vertical glass tube $1.0 m$ long can be adjusted to any position in the tube . A tuning fork vibrating at $660 H z$ is held just over the open top end of the tube . At what positions of the water level will there be resonance . Speed of sound is $330 m / s$ .

Text Solution

Verified by Experts

Resonance corresponds to a pressure antinode at closed end and pressure node at open end. Further , the distance between a pressure node and a pressure antinodes is $λ / 4$ , the condition of resonance would be ,
length of air column
$l = n \frac{λ}{4} = n (\frac{v}{4 f})$
Here , $n = 1, 3, 5, ... .$
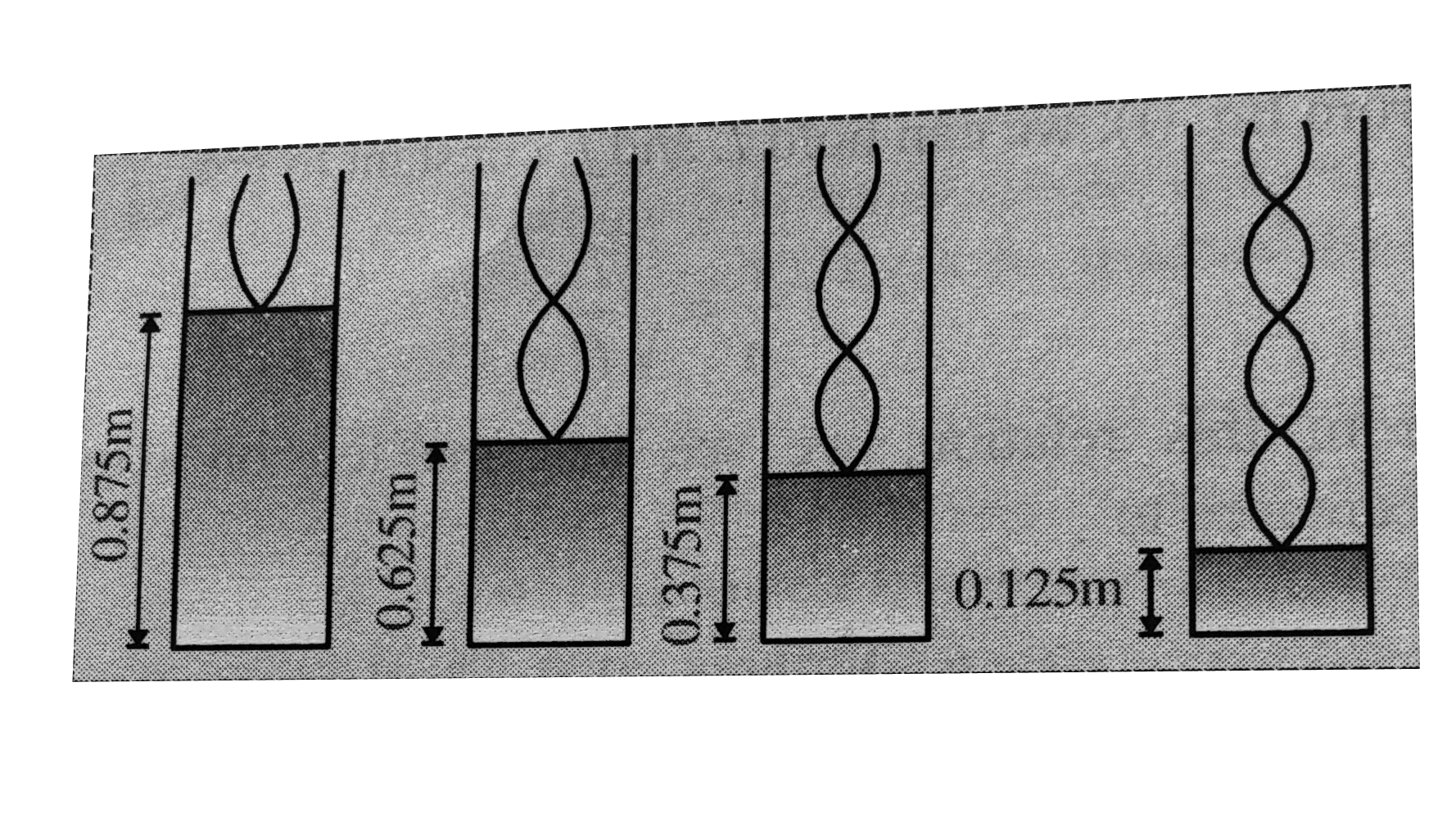
$l_{1} = (1) (\frac{330}{4 \times 660}) = 0.125 m$
and $l_{2} = 3 l_{1} = 0.125 m$
$l_{3} = 5 l_{1} = 0.625 m$
and $l_{4} = 7 l_{1} = 0.875 m$
$l_{3} = 9 l_{1} = 1.125 m$
Since $l_{5} > m$ ( the length of tube), the length of air columns can have the values from $l_{1} \to l_{4}$ only. Therefore , level of water at resonance will be
$(1.0 - 0.125) m = 0.875 m$
$(1.0 - 0.375) m = 0.625 m$
$(1.0 - 0.625) m = 0.375 m$
and $(1.0 - 0.875) m = 0.125 m$
In all the four cases shown in Fig . 7.68, the resonance frequency is $660 H z$ but the first one is the fundamental tone or first harmonic . The second is first overtone or the third harmonic and so on.

Updated on:21/07/2023