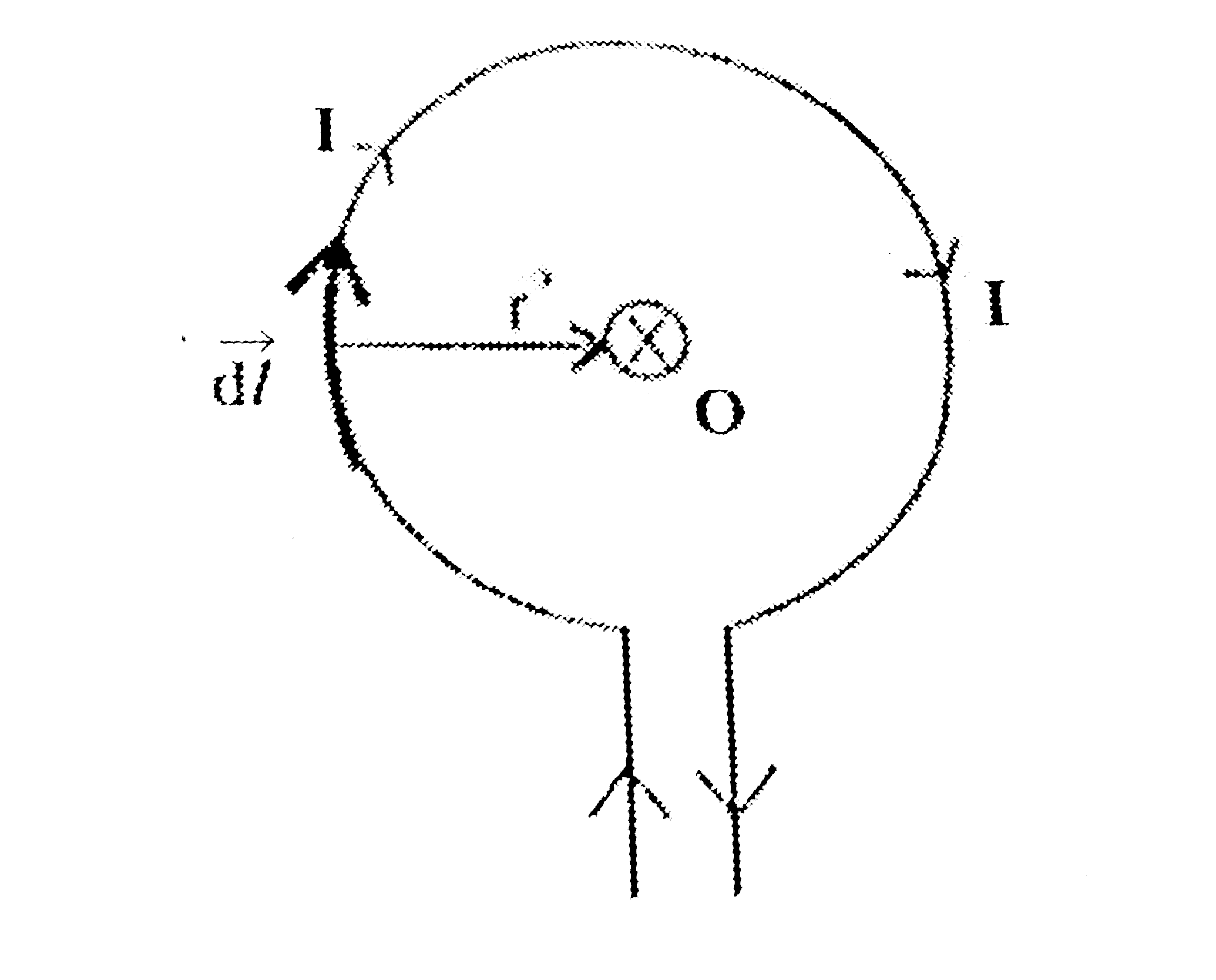
(a) Using Biot-Savart's law, derive an expression for the magnetic field at the centre of a circular coil of radius R, number of turns N, carrying current.
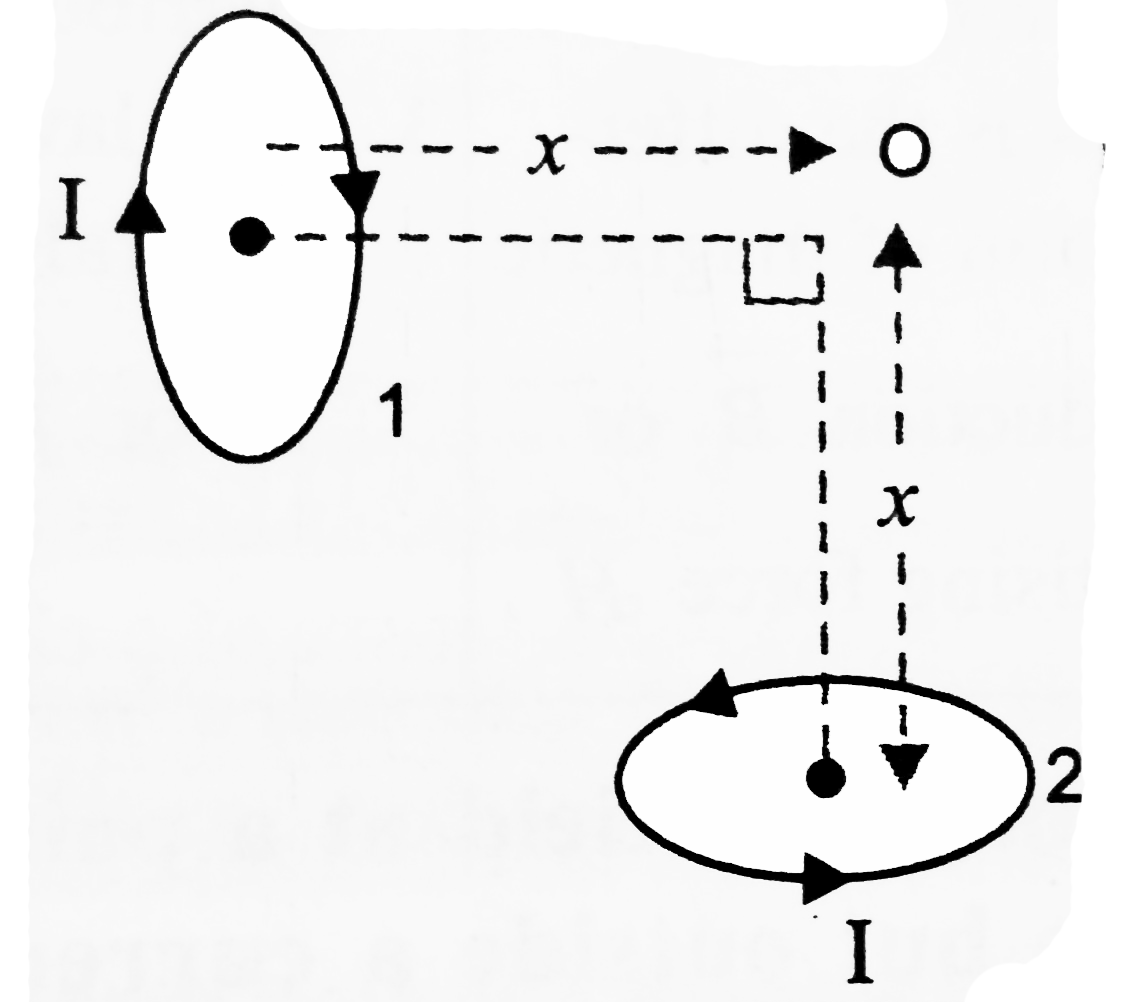
(b) Two small identical circular coils marked 1,2 carry equal currents and are placed with their geometric axes perpendicular to each other as shown in the figure. Derive an expression for the resultant magnetic field at O.

(a) According to Biot-Savart law, the magnetic field due to a current element at the observation point whose position vector is given by
The direction of dl is along the tangent, so dl r. From Biot-Savart law, magnetic field at the Centre O due to this current element is
The magnetic field due to all such current elements will point into the plane of paper at the centre O. Hence the total magnetic field at the centre O is
For a coil of N turns, B .
(b) Magnetic field at O due to loop 1.
, acting towards left
Magnetic field at O due to loop 2.
, acting vertically upwards
Here, R is the radius of each loop.
Resultant field at O will be
This field acts at an angle of with the axis of loop 1.
Topper's Solved these Questions
Similar Questions
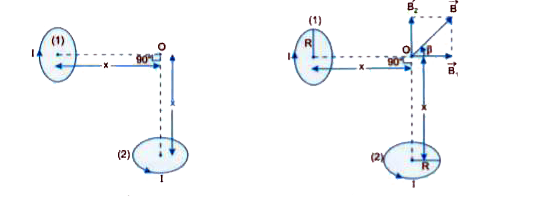
Two small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
 View Solution
View SolutionTwo small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic field at the centre of current carrying coil is
Aμ0ni2rBμ02πnirCμ0ni4rDμ0ni - Question 2 - Select One
The magnetic moment of a current I carrying circular coil of radius ?" and number of turns N varies as
A1r2B1rCrDr2 - Question 3 - Select One
the intensity of the magnetic induction field at the centre of a single turn circular coil of radius 5 cm carrying current of 0.9 A is
A36π×10−7TB9π×10−7TC36π×10−6TD9π×10−6T
The magnetic field at the centre of the current carrying coil
View Solutionthe intensity of the magnetic induction field at the centre of a single turn circular coil of radius 5 cm carrying current of 0.9 A is
View SolutionThe magnetic moment of a current I carrying circular coil of radius r and number of turns N varies as
View SolutionCalculate the magnetic field at the centre of a 100 turn circular coil of radius 10 cm which carries a current of 3. 2 A.
View SolutionWhat is the magnetic induction at the centre of a circular coil of 10 turns, each of radius 5 cm and carrying a current of 5 A ?
View Solution

