State Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.

Video Solution

Text Solution

Verified by Experts

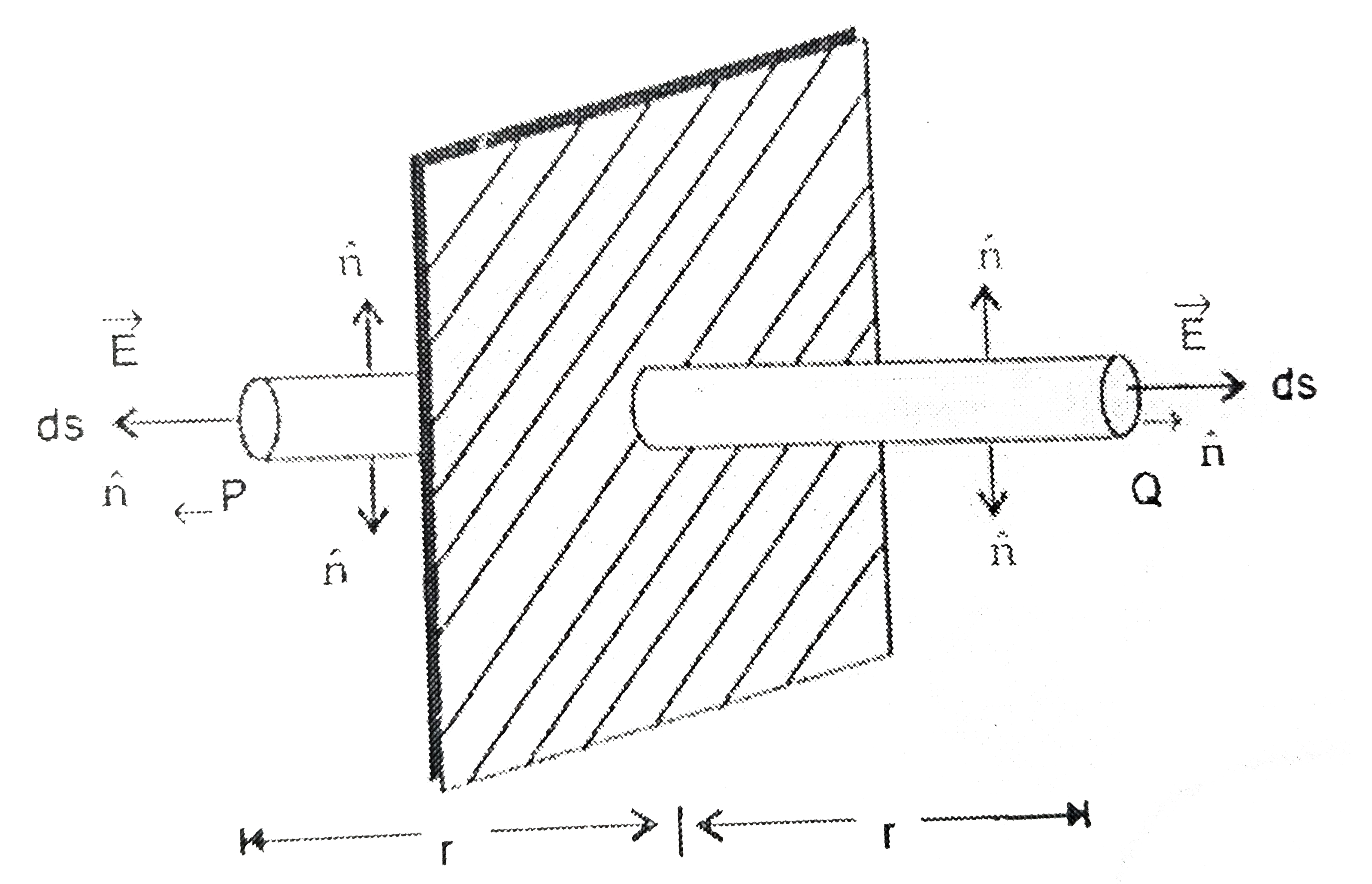
Electric field due to a uniformly charged infinite plane sheet : Suppose a thin non-conducting infinite sheet of uniform surface, charge density $σ$ .
Electric field intensity on either side of the sheet must be perpendicular to the plane of sheet having same magnitude at all points equidistant from sheet.
Let P be any point at a distance r from the sheet.
Let the small area element $\to E = d s ˆ n$
$\to E and ˆ n$ are perpendicular, on the surface of imagined cylinder, so electric flux is zero.
$\to E and ˆ n$ are parallel on the two cylindrical edges P and Q, which contributes electric flux.
$∴$ Electric flux over the edges P and Q of the cylinder is
$2 ϕ = \frac{q}{\in_{0}} \Rightarrow 2 \oint \to E . \to d s = \frac{q}{\in_{0}} [∵ ϕ = \oint \to E . d e c (d s)]$

$2 \oint \to E . \to d s = \frac{q}{\in_{0}}$
$2 \oint E d s = \frac{q}{\in_{0}} [∵ \to E ⊥ \to d s]$
$2 E π r^{2} = \frac{q}{\in_{0}} \Rightarrow E = \frac{q}{2 π \in_{0} r^{2}}$
$∴$ The charge density $σ = \frac{q}{S} \Rightarrow q = π r^{2} σ$ [where S-area of circle]
$E = \frac{π r^{2} σ}{2 π \in_{0} r^{2}} E = \frac{σ}{2 \in_{0}} ∴$ vecotrically $\to E = \frac{σ}{2 \in_{0}} ˆ n$
where $ˆ n$ is a unit vector normal to the plane and going away from it.
When $σ > 0$ , E is directed away from both sides. Hence electric field intensity is independent of r.
When $σ > 0$ , E is directed away from both sides. Hence electric field intensity is independent of r.
Note : For conducting sheet, the surface charge density on both the surface of sheet will be same
$∴ E = \frac{σ}{\in_{0}}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

XII BOARDS PREVIOUS YEAR-XII BOARDS-SET II

Home
Ask Doubt
Profile