State Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
Step-by-Step Solution
Step 1: State Gauss's Law
Gauss's Law in electrostatics states that the total electric flux (Φ_E) through a closed surface (S) is equal to the charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it is expressed as:
ΦE=∮SE⋅dS=Qϵ0
Step 2: Consider the System
We want to find the electric field due to an infinitely long straight wire with a linear charge density λ (in coulombs per meter). We will use a cylindrical Gaussian surface of radius r and length L coaxial with the wire.
Step 3: Calculate the Charge Enclosed
The charge enclosed by the Gaussian surface can be calculated as:
Q=λ⋅L
where λ is the linear charge density (charge per unit length).
Step 4: Determine the Electric Field
Due to the symmetry of the problem, the electric field E at a distance r from the wire will be uniform and directed radially outward. Thus, the electric flux through the cylindrical surface can be simplified:
ΦE=∮SE⋅dS=E⋅A
where A is the curved surface area of the cylinder, which is given by A=2πrL.
Step 5: Substitute into Gauss's Law
Substituting the expressions for the electric flux and the charge enclosed into Gauss's Law gives:
E⋅(2πrL)=λLϵ0
Step 6: Solve for the Electric Field
Now, we can solve for E:
E⋅(2πrL)=λLϵ0
Dividing both sides by 2πrL:
E=λ2πϵ0r
Final Expression
Thus, the electric field E due to an infinitely long straight wire with linear charge density λ is given by:
E=λ2πϵ0r
---
Gauss's Law in electrostatics states that the total electric flux (Φ_E) through a closed surface (S) is equal to the charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀). Mathematically, it is expressed as:
ΦE=∮SE⋅dS=Qϵ0
We want to find the electric field due to an infinitely long straight wire with a linear charge density λ (in coulombs per meter). We will use a cylindrical Gaussian surface of radius r and length L coaxial with the wire.
The charge enclosed by the Gaussian surface can be calculated as:
Q=λ⋅L
where λ is the linear charge density (charge per unit length).
Due to the symmetry of the problem, the electric field E at a distance r from the wire will be uniform and directed radially outward. Thus, the electric flux through the cylindrical surface can be simplified:
ΦE=∮SE⋅dS=E⋅A
where A is the curved surface area of the cylinder, which is given by A=2πrL.
Substituting the expressions for the electric flux and the charge enclosed into Gauss's Law gives:
E⋅(2πrL)=λLϵ0
Now, we can solve for E:
E⋅(2πrL)=λLϵ0
Dividing both sides by 2πrL:
E=λ2πϵ0r
Thus, the electric field E due to an infinitely long straight wire with linear charge density λ is given by:
E=λ2πϵ0r
Topper's Solved these Questions
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET-I
Explore 165 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET-II
Explore 35 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET II
Explore 9 Videos
- SAMPLE PAPER 2019Book:XII BOARDS PREVIOUS YEARChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
State Gauss' law in electrostatic. Using it derive an expression for the electric field due to an infinitely long straight wire of linear charge density λ C/m.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View Solution
Knowledge Check
The electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
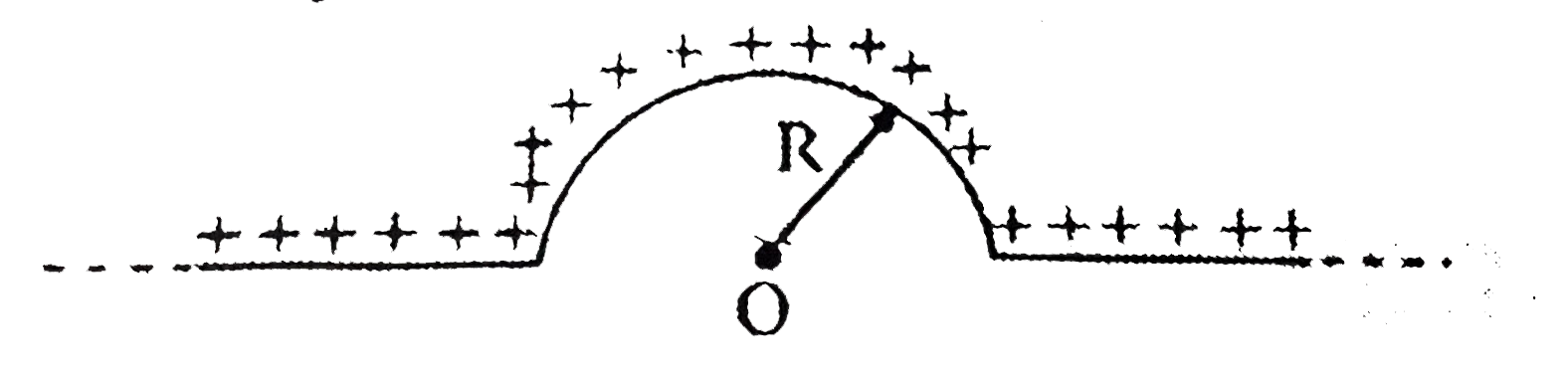 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzeroElectric field of an infinitely long straight wire is proportional to:
ArB1r2C1r3D1r
(a) State Gauss's law. Using this law, obtain the expression for the electric field due to an infinitely long straight conductor of linear charge desntiy λ.
(b) A wire AB of length L has linear charge density λ=kx, where x is measured from the end A of the wire.
This wire is enclosed by a Gaussian hollow surface. Find the expression for the electric flux through this surface.
View SolutionState Gauss' law.Using this law obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ
(ii) A wire AB of length L has linear charge λ=kx, where x is measured from the end A of the wire. The wire is enclosed by a Gaussian hollow surface.Find the expression for the electric flux through the surface.
View SolutionState Gauss's law on electrostatics and derive an expression for the electric field due to a long straight thin uniformly charged wire (linear charge density ) at a point lying at a distance r from the wire.
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionDerive an expression for electric field intensity E due to an infinite place sheet of charge.
View SolutionWrite the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View Solution