Use Gauss's law to derive the expression for the electric field between two uniformly charged large parallel sheets with surface charge densities σ and −σ respectively.
Electric field due to a uniformly charged infinite plane sheet : Suppose a thin non-conducting uniform surface charge density σ.
Electric field intensity →E on either side of the sheet must be perpendicular to the plane of sheet having same magnitude at all points equidistant from sheet.
Let P be any point at a distance r from the sheet. Let the small area element −→dS=dSˆn.
→E and ˆn are perpendicular on the surface of imagined cylinder, so electric flux is zero.
→E and ˆn are parallel on the two cylindrical edges P and Q which contributes electric flux.
∴ Electric flux over the edges Pand Q of the cylinder is
2ϕ=qε0⇒2∮→E−→dS.=qε0
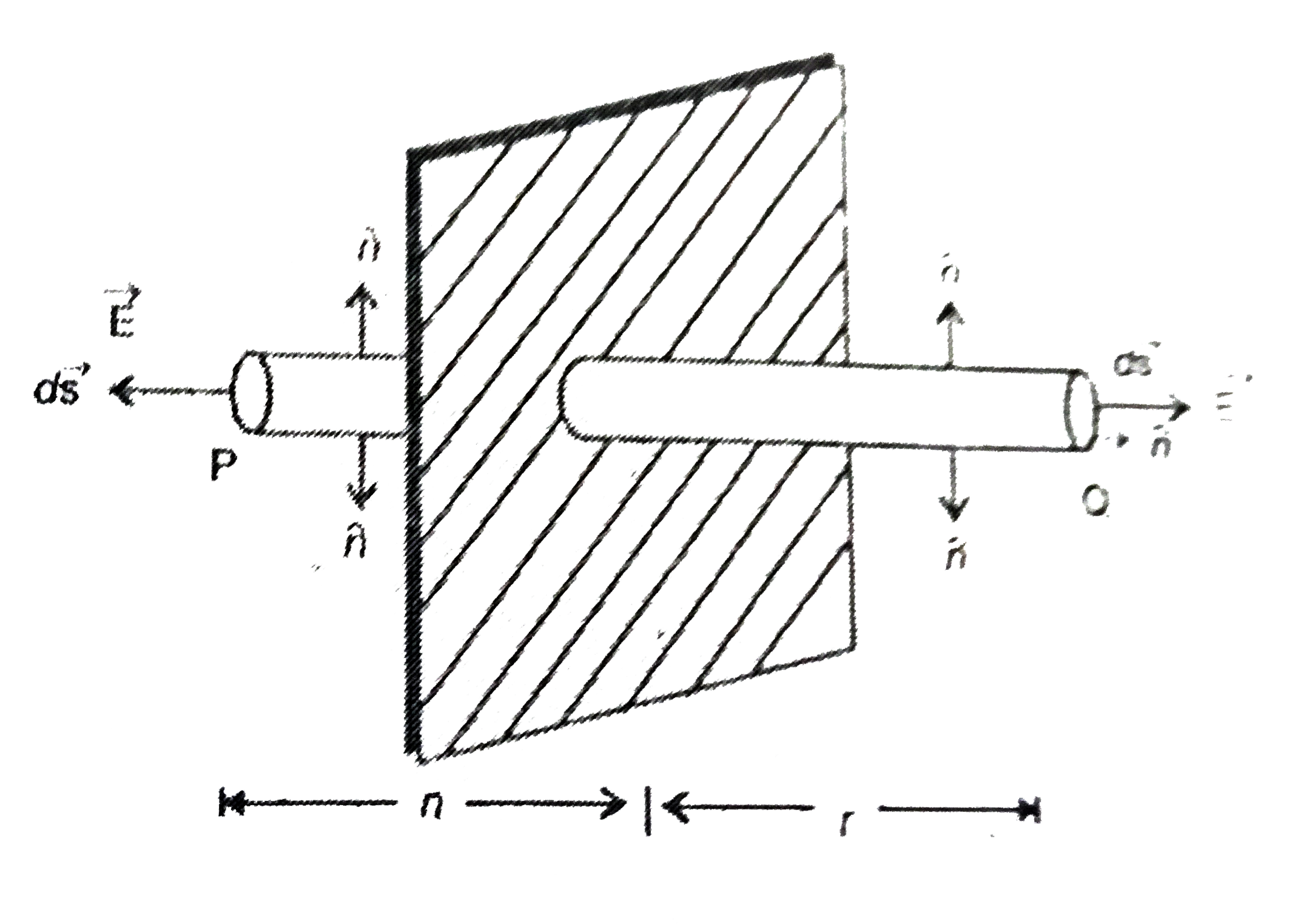
⇒2∮→E−→dS.=qε0
⇒2∮EdS=qε0⇒2Eπr2=qε0⇒E=q2πε0r2
∴ The charge density σ=qS
⇒q=πr2σ
E=πr2σ2πε0r2
E=σ2ε0, vectorically →E=σ2ε0ˆn
Where ˆn is a unit vector normal to the plane and going away from it. where σ>0 E is directed away from both sides.
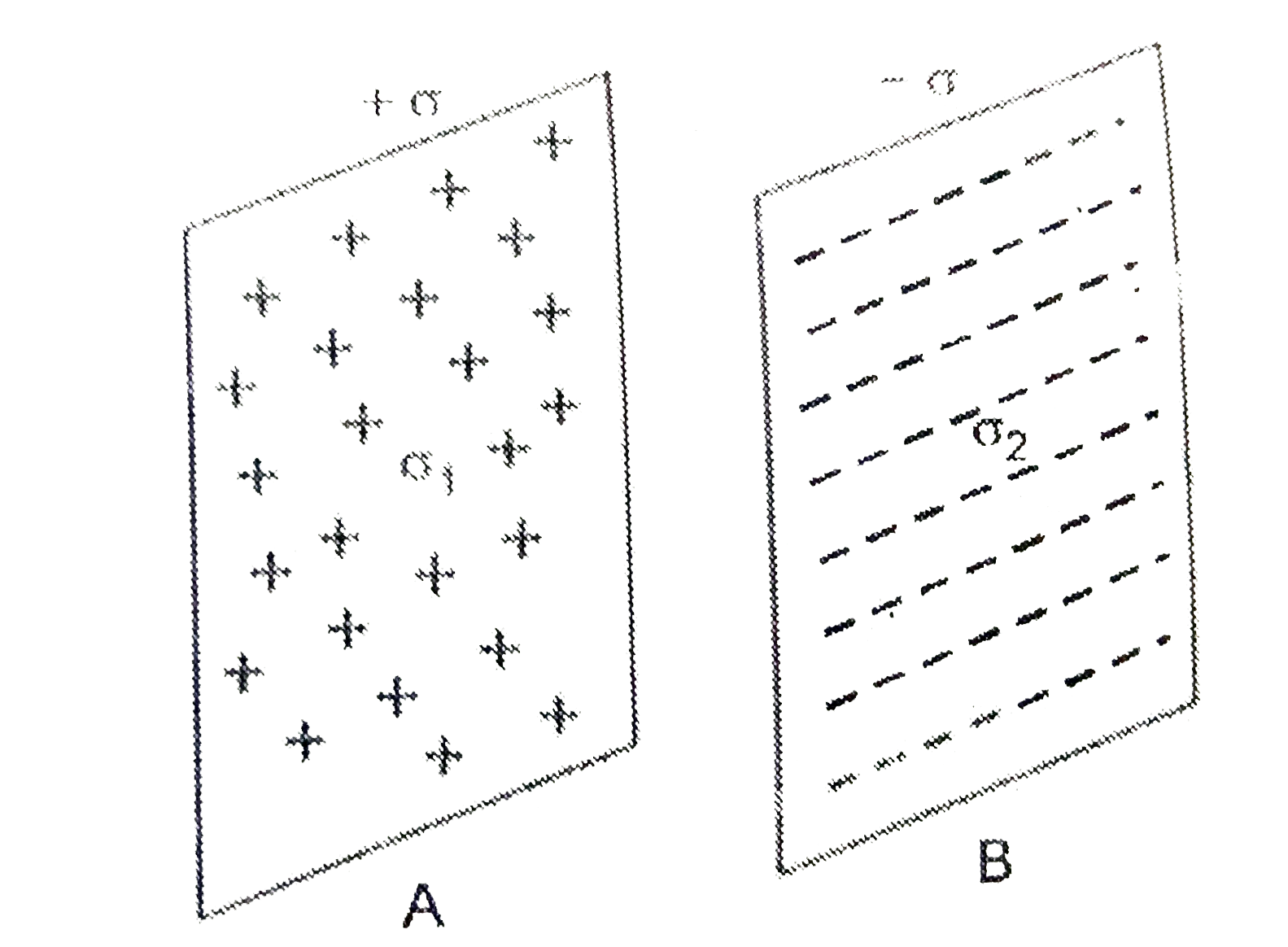
Now consider two infinite plane parallel sheets of charge A and B. Let σ1=σ and σ2=−σ be the uniform surface density of charge on A and B respectively.
The electric field between two plates is given by
E=E1−E2
=σ12ε0−σ22ε0=σ2ε0−(−σ2ε0)=σ+σ2ε0
∴E=2σ2ε0⇒E=σε0.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-III
25 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-III DELHI BOARD
11 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-I
165 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Using Gauss's law, derive an expression for the electric field intensity at any point near a uniformly charged thin wire of charge/length=λC/m.
View Solution(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View Solution(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View SolutionUsing Gauss's law derive an expression for the electric field at any point outside a uniformaly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charges density of the sphere is (i) positive (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100μC/m2 Calculate the
(i) charge on the sphere (ii) total electric flux passing through the sphere.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View Solution
