How does an unpolarised light get polarised when passed through a polarised ?
Two polaroids are set in crossed positions . A third polaroid is placed between the two making an angle $θ$ with the pass axis of the first polaroid . Write the expression for the intensity of light transmitted from the second polaroid . In what orientations will the transmitted intensity be (i) minimum and (ii) maximum ?

Text Solution

Verified by Experts

If an unpolarised light wave is incident on a polaroid then the light get linearly polarised with the electric vector oscillating along a direction perpendicular to the aligned molecules .
If the light from an ordinary source (like a sodium lamp) passes through a polaroid sheet $P_{1}$ , it is observed that its intensity is reduced by half.Rotating $P_{1}$ has no effect on the transmitted beam and transmitted intensity constant .
Let an identical piece of polaroid $P_{2}$ be placed before $P_{1}$ , the light from the lamp is reduced in intensity on passing through $P_{2}$ alone . But rotating $P_{1}$ has effect on the light coming from $P_{2}$ .
In one position , the intensity transmitted by $P_{2}$ followed by $P_{1}$ is nearly zero . When turned by $90^{\circ}$ from this position $P_{1}$ transmits nearly the full intensity emerging from $P_{2}$ as shown in fig.

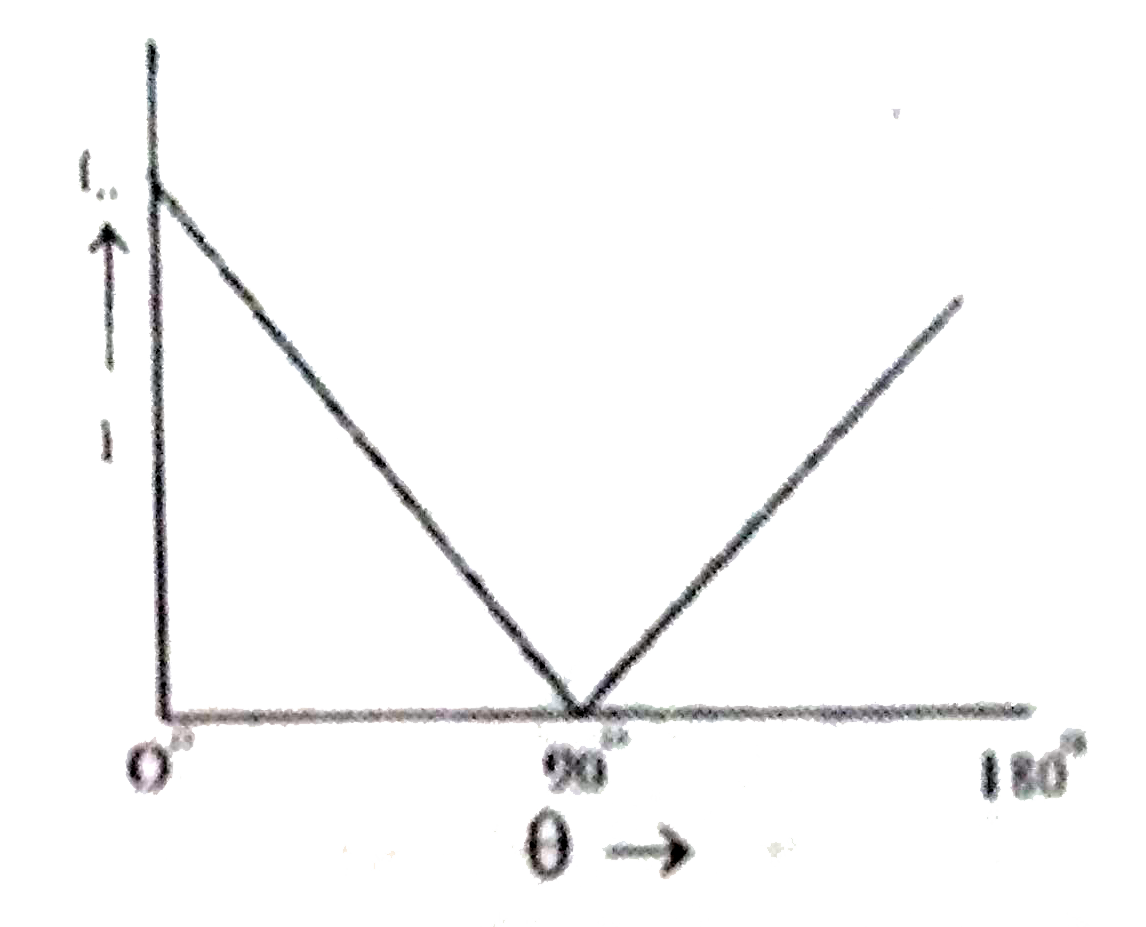
Graph : The graph between intensity of light and the angle between polariser and analyser is shown in the figure .
When the polaroid is rotated in the path of plane polarised light , its intensity will vary from maximum (When the vibrations of the plane polarised light are parallel to the axis of the polaroid ) to minimum (When the direction of vibrations becomes perpendicular to the axis of the crystal).
Let $I_{0}$ be the intensity of polarised light after passing through first polariser $P_{1}$ . Then intensity of light after passing through second polariser $P_{2}$ is given by $I = I_{0} {cos}^{2} θ$ .

Updated on:21/07/2023

Two 'crossed' polaroids A and B are placed in the path of a light-beam. In between these, a third polaroid is C is placed whose polarisation axis makes an angle $θ$ with a polarisation axis of the polaroid A. If the intensity of light emerging from the polaroid a is $I_{o}$ then show that the intensity of light emerging from polaroid B will be $\frac{1}{4} I_{o} {sin}^{2} θ .$
A $\frac{I_{0}}{4} {sin}^{2} 2 ϕ$
B $\frac{I_{0}}{4} {sin}^{2} ϕ$
C $\frac{I_{0}}{4} {cos}^{2} ϕ$
D $\frac{I_{0}}{2} {cos}^{2} 2 ϕ$
Two polaroids are placed in the path of unpolarised light of intensity $I_{0}$ such that no light is emitted from the second polaroid. If a third polaroid, whose pass axis makes an angle $θ$ with the pass axis of first polaroid, is placed between these polaroid then the intensity of the light emerging from the last polaroid will be
A $\frac{I_{0}}{8} {sin}^{2} 2 θ$
B $\frac{I_{0}}{4} {sin}^{2} 2 θ$
C $\frac{I_{0}}{2} {cos}^{4} θ$
D $I_{0} {cos}^{2} θ$