State Faraday's law of electromagnetic induction .
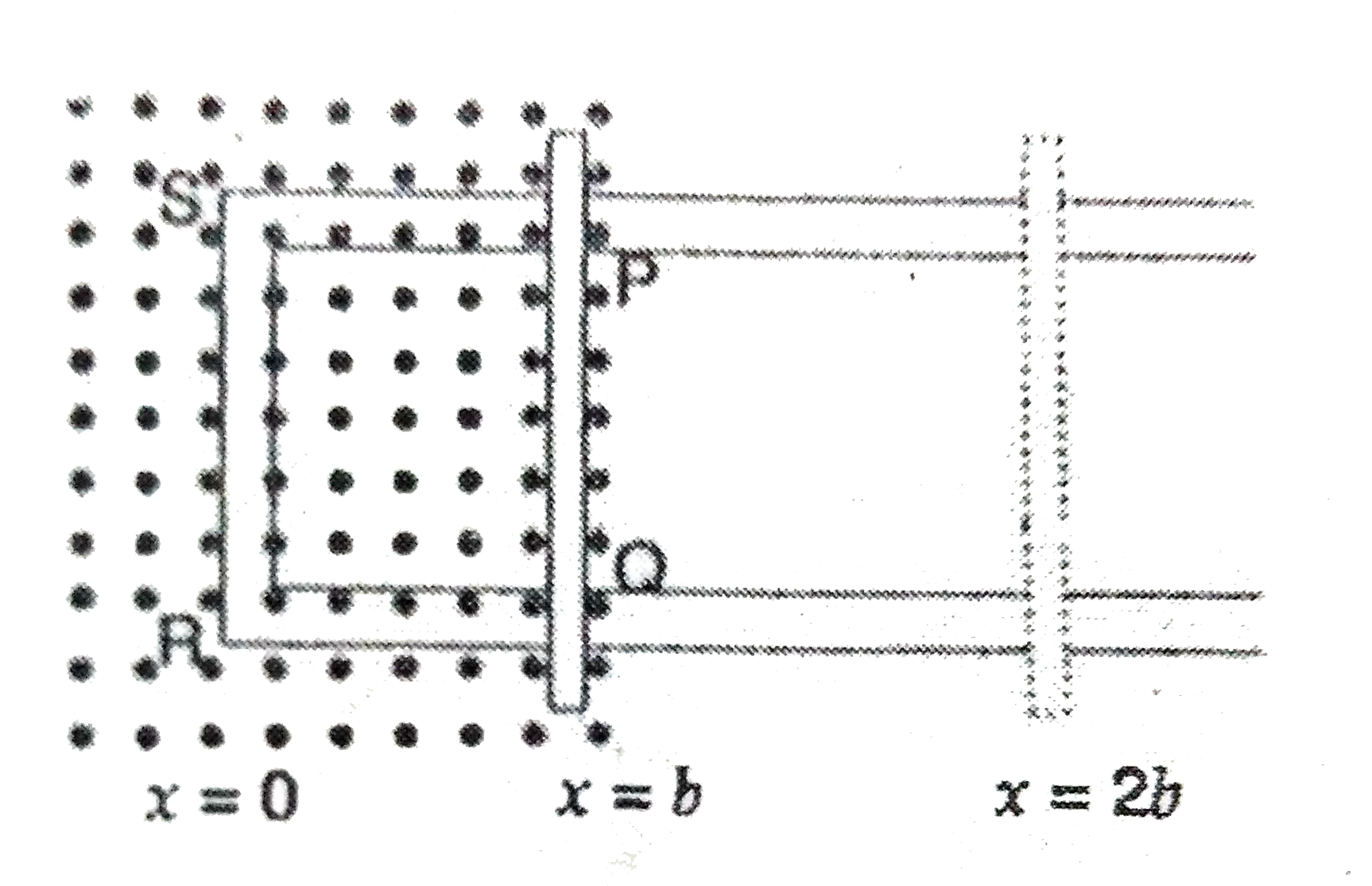
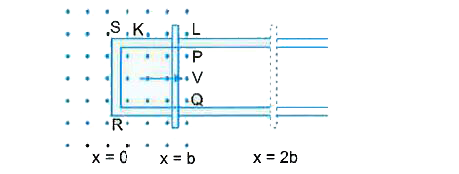
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper . The field extends from x = 0 to x = b and is zero for x>b . Assume that only the arm PQ possesses resistance r . When the arm PQ is pulled outward from x = 0 with constant speed v , obtain the expressions for the flux and the induced emf . Sketch the variations of these quantities with distance 0≤x≤2b .
Part I = Faraday's law of induction : It states that the emf induced in a coil of N turns is directly related to the rate of change of flux through it .
∴ ε=−NdϕBdt
where ϕB is the flux linked with one turn of the coil . if the circuit is closed , a current I=εR is set up in it .
Part II : Refer to following fig(a) . The arm PQ of the rectangular conductor is moved from x = 0 , outwards . The uniform magnetic field is perpendicular to the plane and extends from x = 0 to x = b and is zero the situation when the arm PQ situation when the arm PQ is pulled outwards from x =0 to x = 2b , and is then moved back to x = 0 with constant speed v . Obtain expressions for the flux , the induced emf , the force necessary to pull the arm and the power dissipated as Joule heat . Sketch the variation of these quantities with distance .

Let us first consider the forward motion from x = 0 to x = 2b . The flux Φb linked with circuit SPQR is
ΦB=Bx 0≤x≤b
= Blb b≤x≤2b
The induced emf is ,
ε=−dΦBdt=−Blv,0≤x<b=0,b≤<2b
When the induced emf is non-zero , the current I is IB . Its direction is to the left . In magnitude
F=B2I2vr=0,0≤x<b,b≤x<2b
The joule heating loss is
PI=I2r
=B2I2v2r 0≤x<b
=0 b≤x<2

Topper's Solved these Questions
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET -II
Explore 9 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET -III
Explore 6 Videos
- XII BOARDSBook:XII BOARDS PREVIOUS YEARChapter:XII BOARDSExercise:SET-III DELHI BOARD
Explore 11 Videos
- SAMPLE PAPER 2019Book:XII BOARDS PREVIOUS YEARChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
State Faraday's law of electromagnetic induction.
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper.The field extends from x=0 to x=b and is zero for x>b.Assume that only the arm PQ posses resistance r.When the arm PQ is pulled outward from x=0 with constant speed v, obtain the expressions for the flux and the induced emf. sketch the variations of these quantities with distance 0≤x≤2b.

View SolutionState Faraday's law of electromagnetic induction.
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper.The field extends from x=0 to x=b and is zero for x>b.Assume that only the arm PQ posses resistance r.When the arm PQ is pulled outward from x=0 with constant speed v, obtain the expressions for the flux and the induced emf. sketch the variations of these quantities with distance 0≤x≤2b.

View Solution
Knowledge Check
A conductor PQ , with PQ=r , moves with a velocity v in a uniform magnetic field of induced B . The emf induced in the rod is
A(→v×→B).→rB→v.(→r×→B)C→B.(→r×→v)D∣∣→r×(→v×→B)∣∣
(a) State Faraday's law of electromagnetic induction.
(b) Figure 6.60 shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper. The field extends from x = 0 to x =b and is zero for >b. Assume that only the arm PQ possesses resistance r. When the arm PQ is pulled outward from x =0 to x = 2b and is then moved backward to x = 0 with constant speed v, obtain the expressions for the flux and the induced emf. Sketch the variations of these quantities with distance 0≤x≤2b.
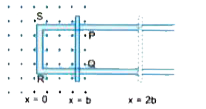
View SolutionThe arm PQ of the rectangular conductor is moved from x=0, outwards in the uniform magnetic field which extends from x=0 to x=b and is zero for x>b as shown. Only the arm PQ possess substantial resistance r. Consider the situation when the arm PQ is pulled outwards from x=0 to x=2b, and is then moved back to x=0 with constant speed v. Obtain expression for the flux, the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat. Sketch the variation of these quantities with distance.
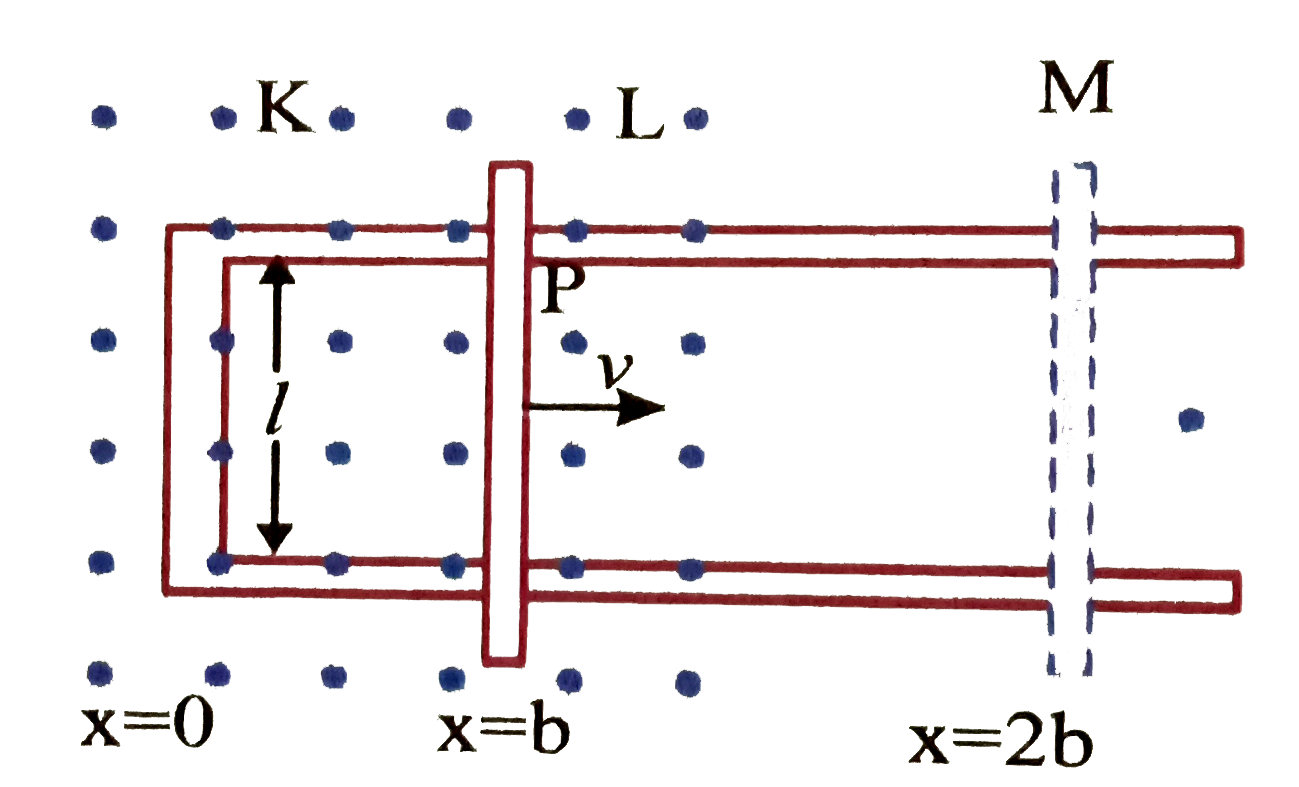
View SolutionIn the following diagram, the arm PQ of the rectangular conductor is moved from x = 0 ,
outwards.
The unfirom magnetic field is perpendicular to the plane and extends from x=0 to x=b and is zero for x>b. Only the arm PQ possesses substantial resistance 'r'. Consider the situation when the arm PQ is pulled outwards from x = 0 to x = 2b, and then moved back to x = 0 with constant speed 'v'. Obtain expressions from the (i) magnetic flux, (ii) the induced emf, (iii) the force necessary to pull the arm and (iv) the power dissipated as joule heat.
Sketch the variation of these quantities with distance.
View SolutionThe arm PQ of the rectangular conductor is moved from x=0, outwards in the uniform magnetic field which extends from x=0 to x=b and is zero for x>b as shown. Only the arm PQ possess substantial ressitance r. Consider the situation when the arm PQ is pulled outwards from x=0 to x=2b, and is then moved back to x=0 with constant speed v. Obtain expression for the flux, the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat. Sketch the variation of these quantities with distance.

View SolutionFigure shows a rectangular loop conducting PQRS in which the arm PQ is free to move. A uniform magnetic field acts in the direction perpendicular to the plane of the loop. Arm PQ is moved with a valocity v towards the arm RS. Assuming that the arms QR, RS and SP have negligible resistances and the moving arm PQ has the resistance r, obtain the expression for (i) the current in the loop (ii) the force and (iii) the power required to move the arm PQ.

View SolutionFigure shows a rectangular loop conducting PQRS in which the arm PQ is free to move. A uniform magnetic field acts in the direction perpendicular to the plane of the loop. Arm PQ is moved with a valocity v towards the arm RS. Assuming that the arms QR, RS and SP have negligible resistances and the moving arm PQ has the resistance r, obtain the expression for (i) the current in the loop (ii) the force and (iii) the power required to move the arm PQ.

View SolutionFig. 6.50 shows a rectangular conducting loop PQRS in which the arm PQ is free to move. A uniform magnetic field acts in the direction perpendicular to the plane of the loop. Arm PQ is moved with a velocity v towards the arm RS. Assuming that the arms QR, RS and SP have negligible resistances and the moving arm PQ has the resistance r, obtain the expression for the current in the loop (ii) the force and (iii) the power required move the arm PQ.
View Solution
