Derive the expression for the average power disspated in a series LCR circuit for an ac source of a voltage, v=vmsinωt, carrying a current, i=imsin(ωt+ϕ).
Hence, define the them ''Wattless current''. State under what condition it can be realized in a circuit.
V=Vmsinωt
I=Imsin(ωt+ϕ)
The instantaneous power is given by
P=VI=VmImsinωtsin(ωt+ϕ)
=VmIm2=[2sinωtsin(ωt+ϕ)]
=VmIm2[cosϕ−cos(2ωt+ϕ)]
The second term inside bracked is time dependent so, its average over a cycle is zero.
So, 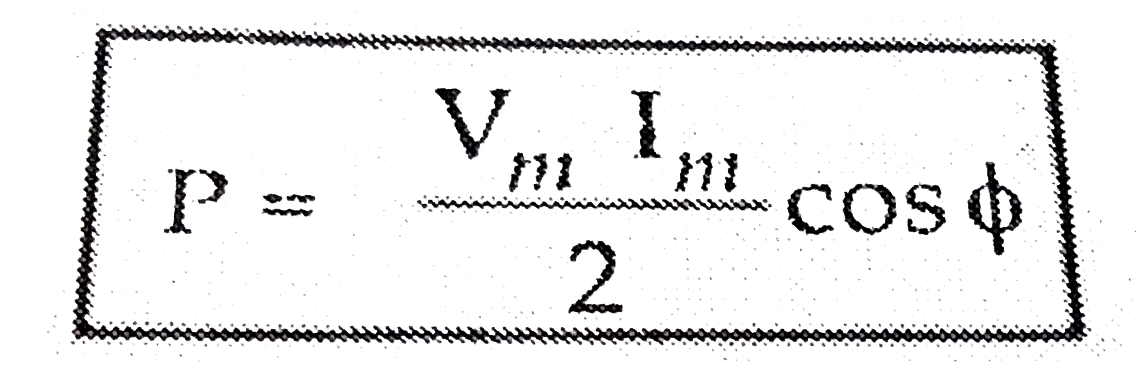
Wattless currecnt : The current in a.c. circuit is said to be wattless if the average power consumed in the cuicuite is zero.
For example, when secondary of the transformer is open the current in the primary is almost wattless.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-D
4 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-E
4 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-B
6 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
(a) Deriver and expression for the average power consumed in a series LCR circuit connected to a.c., source in which the phase different between the voltage and the current in the circuit is ϕ.
(b) Define the quality factor in an a.c. circuit. Why should the quality factor have high value in receiving circuits ? Name the factors on which it depends.
View Solutiona) Derive the expression for the current flowing in an ideal capacitor and its reactance when connected to an ac source of voltage V=V0sinωt
b) Draw its phasor diagram.
c) If resistance is added in series to capacitor what changes will occur in the current flowing in the circuit and phase angle between voltage and current.
View Solution
Knowledge Check
The power dissipated in alternating circuit with voltage e=e0 sin ωt and current I=I0sin(ωt−ϕ) is
Ae0I0BermsIrmscosϕCermsIrmsD0The instantaneous current in a circuit is, I=sin(ωt+ϕ) ampere. What is the r.m.s., value of the current?
A2AB√2AC1AD1/√2AIn a series L.C.R. circuit alternating emf (v) and current (i) are given by the equation v=v0sinωt, i=i0sin(ωt+π3) The average power dissipated in the circuit over a cycle of AC is
Av0I02Bv0I04C√32v0I0Dzero
What is the power dissipation in an AC circuit in which voltage and current are given by V=300sin(ωt+π2) and I = 5 sinωt ?
View SolutionIn the circuit shown the source voltage is given asv=V0 sin ωt. Find the current through the source as a function of time.
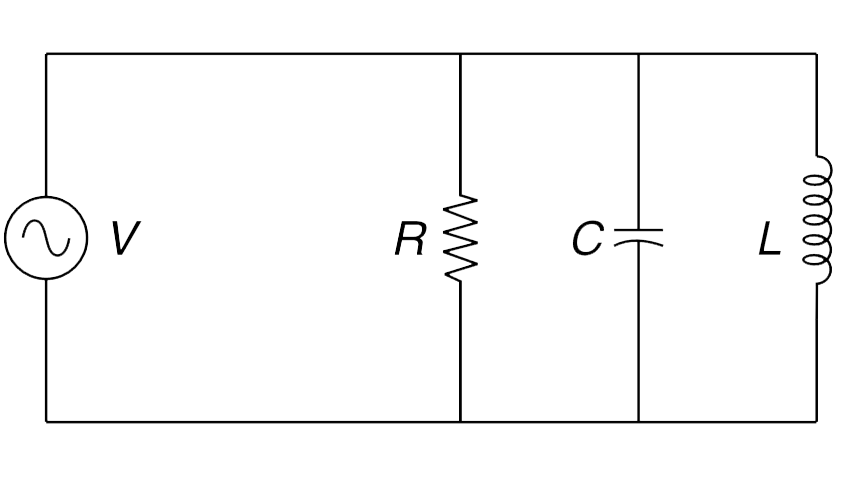
View SolutionThe voltage and current in a series AC circuit are given by V=V0cosωtandI=i0sinωt.
What is the power dissipated in the circuit?
View SolutionThe voltage and current in a series AC circuit are given by
V=V0cosωtandI=i0sinωt.
What is the power dissipated in the circuit?
View SolutionDraw the phasor diagram of a series LCR connected across an ac source V=V0sinωt. Hence derive the expression for the impedance of the circuit . Obtain the conditions for the phase angle under which the current is (i) maximum and (ii) minimum.
View Solution
