Obtain the expression for the magnetic energy stored in an ideal inductor of self inductance L when a current I passes through it.
Hence obtain the expression for the energy density of magentic field produced in the inductor.
Work done aginst the induced emf in building up the current O to I in
W=∫dw=∫Eldt=∫Ldldt.ldt
⇒I∫0LIdI=12LI2
This is magnetic energy stored in solenoid.
UB=W=12LI2=12L(Bμ0n) [∵B=μ0nI]
UB=12μ0n2Al(Bμ0n)2 [∵L=μ0n2Al]
So, magnetic energy density UB=UBAl⇒UB⇒B22μ0.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-D
4 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-E
4 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SECTIONS-B
6 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Calculate the energy stored in an inductor of inductance 50 mH when a current of 2.0 A is passed through it.
View Solution(a) Derive the expression for the magnetic energy stored in an inductor when a current I develops in it. Hence, obtain the expression for the magnetic energy density.
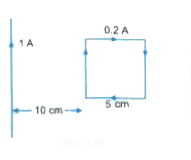
(b) A square loop of sides 5 cm carrying a current of 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinitely long wire carrying a current of 1 A as shown in Fig. 6.66. Calculate (i) the resultant magnetic force, and (ii) the torque, if any, acting on the loop.
View Solution
Knowledge Check
The energy stored in an inductor of self inductance L carrying current l, is given by
ALl2B−Ll2C12Ll2D−12Ll2The energy stored in an inductor of self-inductance L henry carrying a current of I ampere is
A1/2L2IB1/2LI2CLI2DL2IAverage energy stored in a pure inductance L when current i flows through it, is
ALi2B2Li2CLi24DLi22
Starting from the expression for the energy W=1/2LI2, stored in a solenoid of self-inductance L to build up the current I, obtain the expression for the magnetic energy in terms of the magnetic field B, area A and length l of the solenoid having n number of turns per unit length. Hence, show that the energy density is given by B2/2μ0.
View SolutionWhat is expression for magnetic energy stored in an inductor. Compare it with the electrostatic energy stored in a capacitor.
View SolutionEnergy stored in an inductor is proportional to (i = current in the inductor)
View SolutionIn what form is the energy stored in an inductor or A coil of inductance L is carrying a steady current i . What is the nature of its stored energy
View SolutionIn an inductor of inductance L=100mH, a current of I=10A is flowing. The energy stored in the inductor is
View Solution
