(i) Derive the expression for the specific for the electric potential due to an electric dipole at a point on its axial line.
(ii) Depiet the equivpotential surfaces due to an electric dipole.

Text Solution

Verified by Experts

(i) Expression : Potential at P due to charge $+ q$ and -q.
$V_{- q} = \frac{- q}{4 π \in_{0} r_{1}}$ and $V_{+ q} = \frac{q}{4 π \in_{0} r_{2}}$
Potential at P due to dipole $V = V_{- q} + V_{+ q} = \frac{q}{4 π \in_{0}} [\frac{1}{r_{2}} - \frac{1}{r_{1}}] \dots\dots.. (i)$

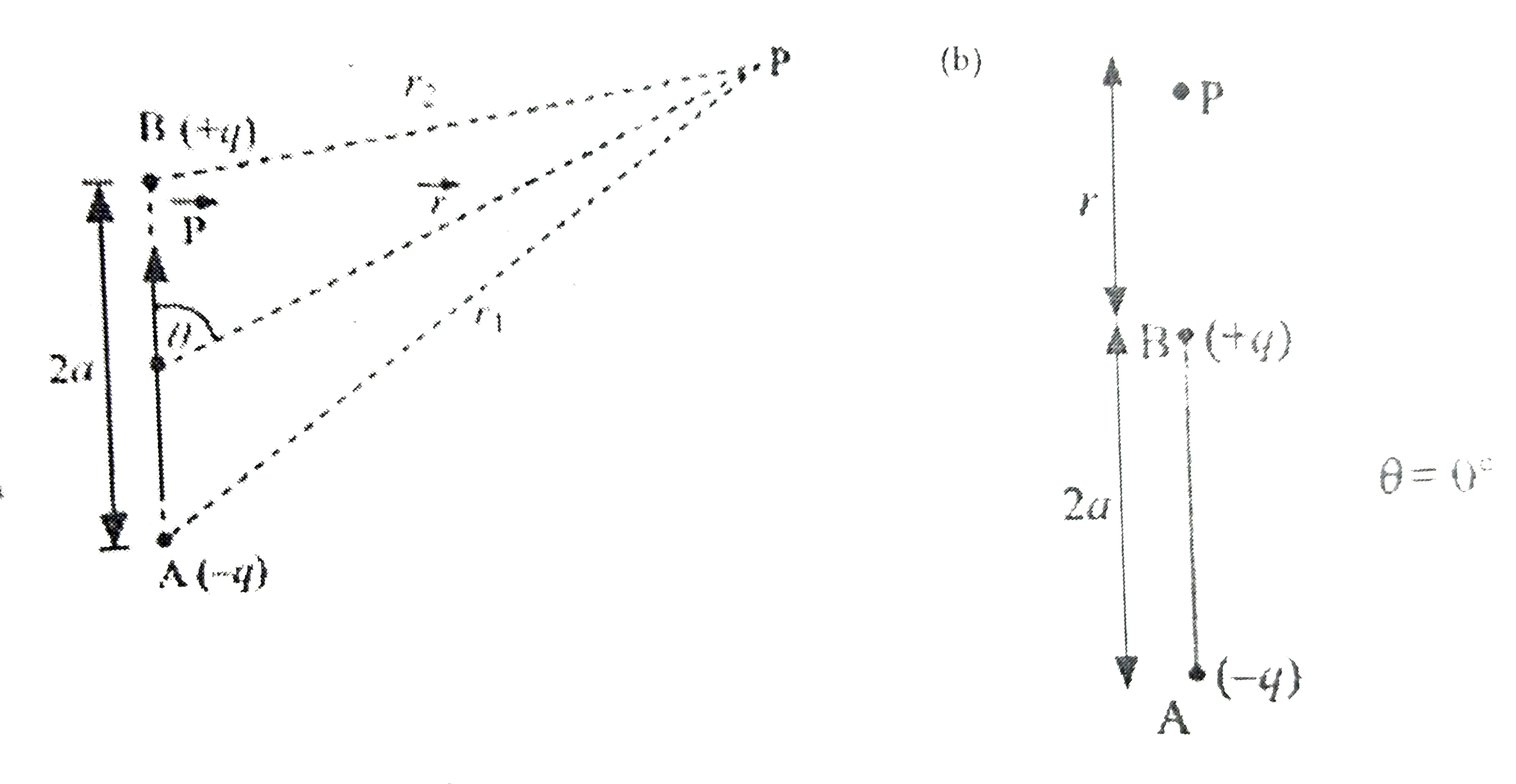
From the figure, $r_{1}^{2} = r^{2} + d + 2 a r cos θ$
and, $r_{2}^{2} = r^{2} + a^{2} + 2 a r cos (180^{\circ} - θ) = r^{2} + a^{2} - 2 a r cos θ$
$\Rightarrow r_{1}^{2} = r^{2} [1 + \frac{a^{2}}{r^{2}} + \frac{2 a}{r} cos θ] = r^{2} [1 + \frac{2 a}{r} cos θ]$ as $r > > a, \frac{a^{2}}{r^{2}} = 0$
$\Rightarrow r_{1} = r {[1 + \frac{2 a}{r} cos θ]}^{\frac{1}{2}}$
So $\frac{1}{r_{1}} = \frac{1}{r} {[1 + \frac{2 a}{r} cos θ]}^{- \frac{1}{2}}$
and $\frac{1}{r_{2}} = = \frac{1}{r} {[1 - \frac{2 a}{r} cos θ]}^{- 1 / 2}$
Using it for $(i)$
$V = \frac{q}{4 π \in_{0} r} [1 + \frac{a}{r} cos θ - (1 - \frac{a}{r} cos θ)]$
[Applying Binomial Theorem and neglecting highest power of $\frac{2 a}{r}$ ]
Hence, $V = \frac{q}{4 π \in_{0} r} [1 + \frac{q}{r} cos θ - 1 + \frac{a}{r} cos θ]$
$= \frac{q \times 2 a cos θ}{4 π \in_{0} r^{2}}$
$\Rightarrow V = \frac{p cos θ}{4 π \in_{0} r^{2}}, {p = q \times 2 a = dipole moment}$
Vaxial $= \frac{p cos θ}{4 π \in_{0} r^{2}}$ ( $∵ θ = 0^{\circ}$ on axial line) $= \frac{p}{4 π \in_{0} r^{2}}$
(ii) $V_{net} = V_{A} + V_{B} = \frac{- k q}{(r^{2} + a^{2})} + \frac{- k q}{(r^{2} + a^{2}) = 0}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

XII BOARDS PREVIOUS YEAR-XII BOARDS-SET-II DELHI BOARD (SEC-C)

Home
Ask Doubt
Profile