(a) Use Gauss's law to derive the expression for the electric filed $(\vec{E})$ due to straight uniformaly charges infinite line of charges density $λ C / m$ .
(b) Draw a graph to show the variation of E with perpendicular from the line of charge.
(c) Find the work done in brining a charge q from prependicular distance $r_{1}$ to $r_{2} (r_{2} > r_{1})$ .

Text Solution

Verified by Experts

(a)
$O = \oint \vec{E} . d \vec{a}$
$O = \int E . d a_{1} {\cos 90}^{\circ} + \int \vec{E} . d {\vec{a}}_{2} {\cos 0}^{\circ} + \int \vec{E} . d {\vec{a}}_{3} {\cos 90}^{\circ}$
$O = \int E d a_{2}$
$O = E_{2} π r l_{1}$
$O = \frac{\sum q}{\sum_{0}} = \frac{λ l_{1}}{\sum_{0}}$
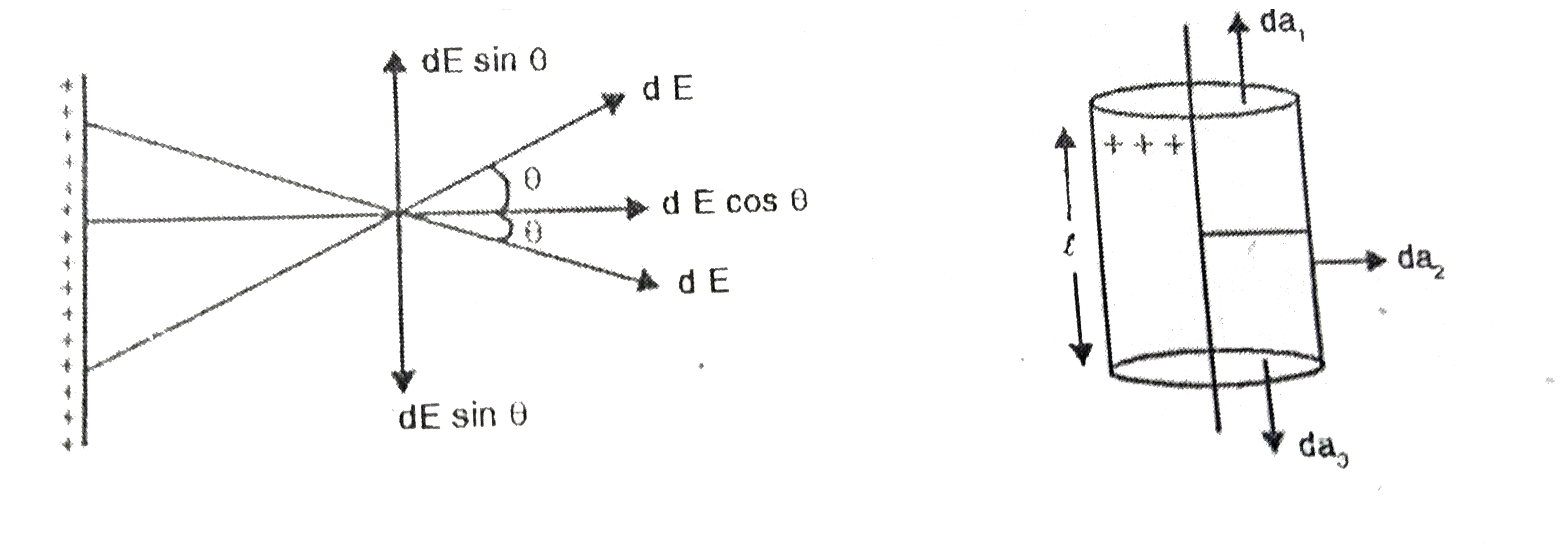
Equate them : $\frac{d l_{1}}{\sum_{0}} = E_{2} π r l_{1}$
$E = \frac{λ}{2 π r \sum_{0}}$
(b)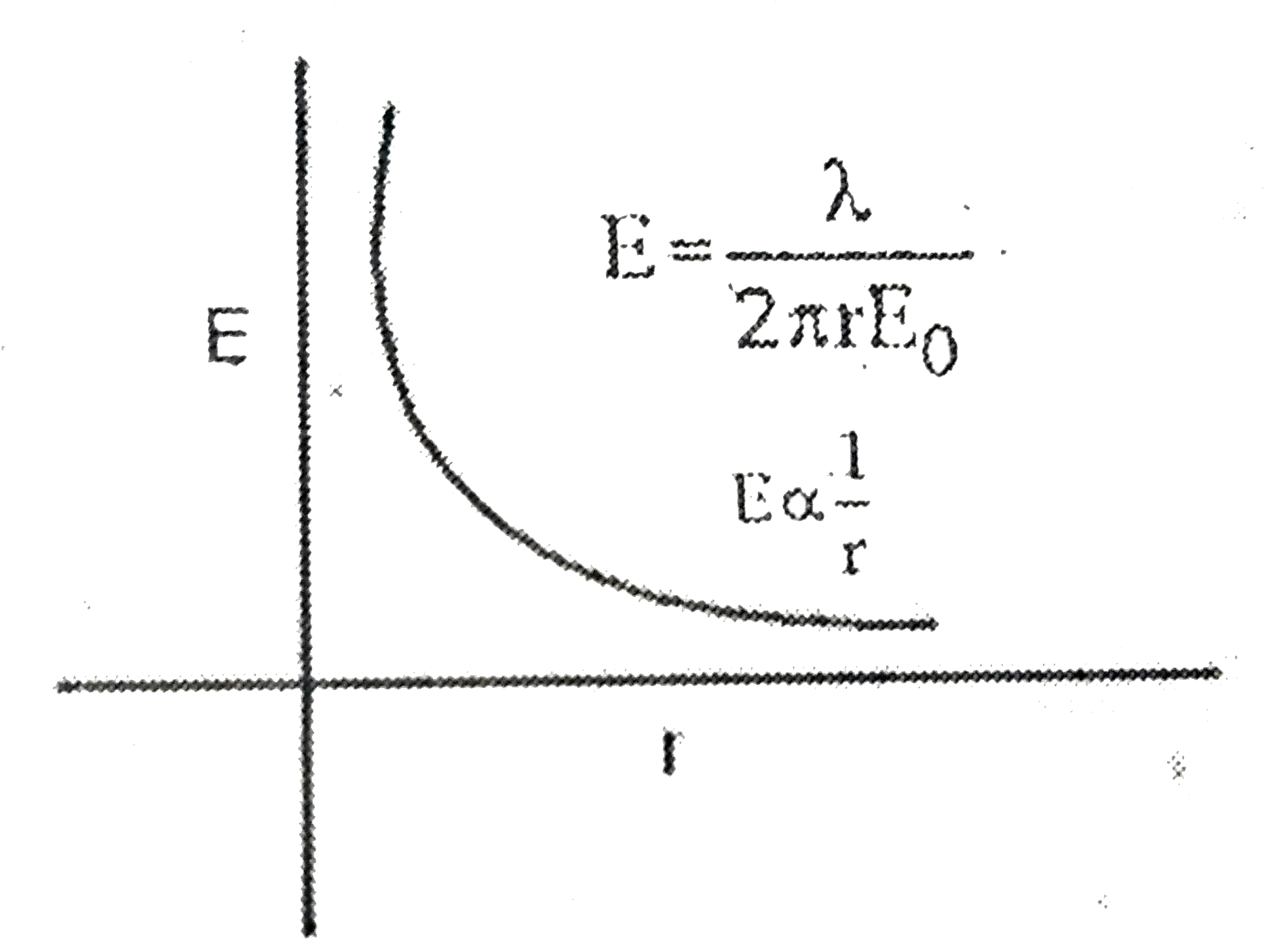
(c) Work done to moving from $r_{1}$ to $r_{2} d v \underset{r_{1}}{\int^{r_{2}}} \frac{λ}{2 π \sum_{0} r} d r$
$d v = \frac{λ}{2 π r \sum_{0}} \underset{r_{1}}{\int^{r_{2}}} \frac{1}{r} d r$
$O = \frac{λ}{2 π \sum_{0}} - [\log . \frac{r_{2}}{r_{1}}]$
$w = 9 V$
$w = 9 (\frac{λ}{2 π \sum_{0}} \log (\frac{r_{2}}{r_{1}}))$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile