An eppipse of eccentricity (2sqrt2)/(3) is inscribed in a circle and a

Topper's Solved these Questions

BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPER 3EXERCISE - CATEGORY 2 : SINGLE OPTION CORRECT TYPE
15videos
MODEL TEST PAPER 3
BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPER 3EXERCISE - CATEGORY 3 : One or More than One Option Correct Type
10videos
MODEL TEST PAPER 3
BOOK - MTG-WBJEECHAPTER - MODEL TEST PAPER 2EXERCISE - CATEGORY 3 : One or More than One Option Correct Type
10videos
MODEL TEST PAPER 2
BOOK - MTG-WBJEECHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - WB JEE Previous years questions (Category 3 : More than One Option correct type)
1videos
PERMUTATIONS AND COMBINATIONS

Knowledge Check

Question 1 - Select One
An ellipse of eccentricity $\frac{2 \sqrt{2}}{3}$ is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is
A $\frac{1}{2}$
B $\frac{2}{3}$
C $\frac{1}{9}$
D $\frac{2}{9}$
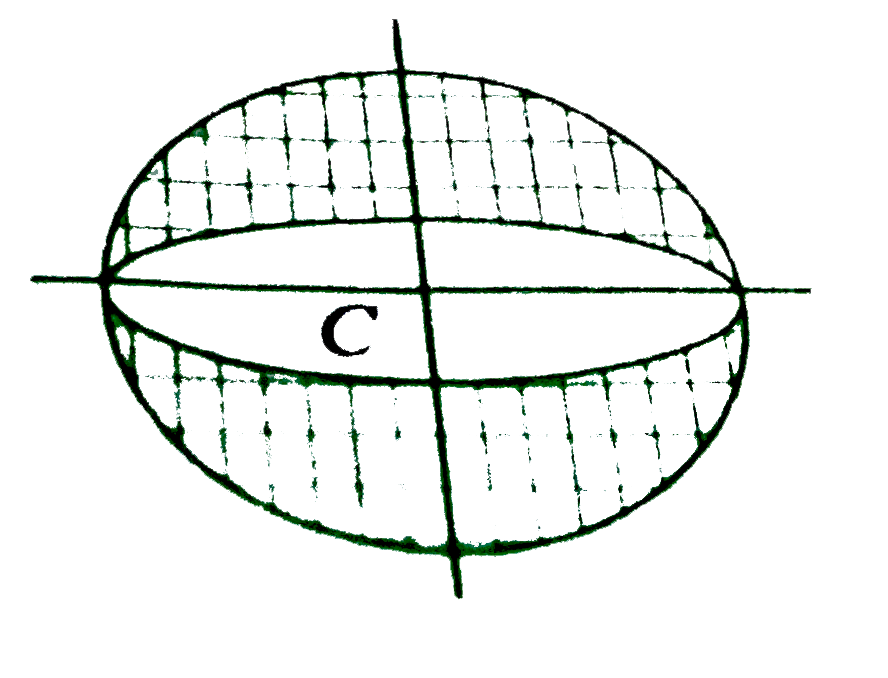
Question 2 - Select One
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity $2 \sqrt{2} / 3$ is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
$1 - \frac{b^{2}}{a^{2}} = \frac{8}{9} or \frac{b^{2}}{a^{2}} = \frac{1}{9}$
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
$p = \frac{Area of shaded region}{Area of circle}$
$= \frac{π a^{2} - π a b}{π a^{2}} = 1 - \frac{b}{a} = 1 - \frac{1}{3} = \frac{2}{3}$
Now, answer the following questions.

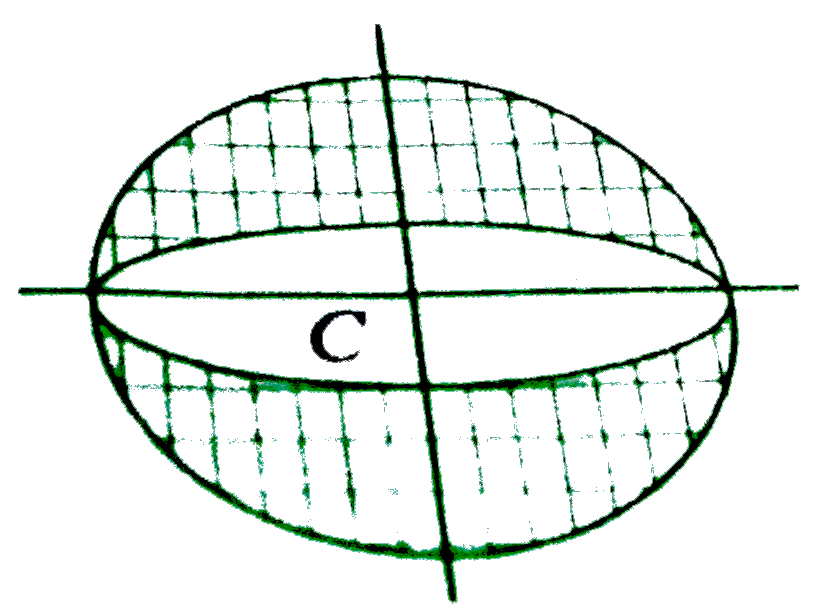
A point is selected at random inside a circle. The probability that the point is closer to the center of the circle than to its circumference is
A $1 / 4$
B $1 / 2$
C $1 / 3$
D $1 / \sqrt{2}$
Question 3 - Select One
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity $2 \sqrt{2} / 3$ is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
$1 - \frac{b^{2}}{a^{2}} = \frac{8}{9} or \frac{b^{2}}{a^{2}} = \frac{1}{9}$
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
$p = \frac{Area of shaded region}{Area of circle}$
$= \frac{π a^{2} - π a b}{π a^{2}} = 1 - \frac{b}{a} = 1 - \frac{1}{3} = \frac{2}{3}$
Now, answer the following questions.

Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is
A $1 / 3$
B $1 / 3$
C $2 / 3$
D $5 / 9$

An eppipse of eccentricity $\frac{2 \sqrt{2}}{3}$ is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is

The correct Answer is:D

Topper's Solved these Questions

Similar Questions

Knowledge Check

An ellipse of eccentricity $\frac{2 \sqrt{2}}{3}$ is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is

MTG-WBJEE-MODEL TEST PAPER 3-CATEGORY 3 : One or More than One Option Correct Type

An eppipse of eccentricity 2 2 3 is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is

The correct Answer is:D

Topper's Solved these Questions

Similar Questions

Knowledge Check

An ellipse of eccentricity 2√23 is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is

MTG-WBJEE-MODEL TEST PAPER 3-CATEGORY 3 : One or More than One Option Correct Type

An eppipse of eccentricity $\frac{2 \sqrt{2}}{3}$ is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is

An ellipse of eccentricity $\frac{2 \sqrt{2}}{3}$ is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is