A particle projected with velcoity v0 strikes at right α plane through the point of projection .
Let α be the angle between the velocity of projection and the inclined plane .
vax=v0cosα,vay=v0sinα
ax=gβ,ay=−gcosβ
⇒Vx(t)=v0cosα−gsinβt
At the point of impact vx⇒t=v0cosαgsinβ ....(i)
Also y at the point is zero .
⇒v0sinα−12gcosβt2=0⇒t=2v0sinαgcosβ ....(ii)
From (i) and (ii) v0cosαgsinβ=2v0sinαgcosβ
tanα=12cotβ
x=v0=cos(α+β)t
=v0[cosαcosβ−sinαβ]v0cosαgsinβ=V20g[cos2αcotβ−sinαcosα]
=v20g⎡⎣(2√4+cot2β)2cotβ−cotβ√4+cot2β2√4+cot2β⎤⎦
(using tanα=12cotβ) = v20g2cotβ4+cot2β
From figure
∴y=xtanβ=v20g.2cotβ4+cot2βtanβ⇒y=2V20g(4+cot2β)
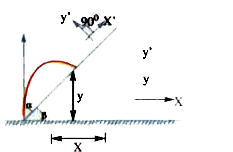
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS6videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS10videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)7videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
Similar Questions
A particle projected with velcoity v0 strikes at right α plane through the point of projection .
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View Solution
Knowledge Check
- Question 1 - Select One
A perfectly elastic particle is projected with a velocity v on a vertical plane through the line of greatest slope of an inclined plane of elevation α.If after striking the plane, the particle rebounds vertically show that it will return to the point of projection at the end of time equal to
A6vg√1+8sin2αB6vg√1+sin2αCvg√1+8sin2αDvg√1+sin2α - Question 2 - Select One
A parojectile of mass 1kg is projected with a velcoity of √20m/s such that it strikes on the same level as the point of projection at a distance of √3m. Which of the following options are incorrect:
AThe maximum height reached by the projectile can be 0.25m.Bthe minimum velocity during its motion can be √15m/sCthe time taken for the flight can be √35sec.Dmaximum potential enegry during its motion can be 6J. - Question 3 - Select One
A particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
A30∘+tan−1(√32)B45∘C60∘D30∘+tan−1(2√3)
A particle of mass m is projected with a speed v0 at an angle of projection θ with horizontal. Find the torque of the weight of the particle about the point of projection after time v0sinθg
View SolutionA particle is projected with a velocity ¯v=aˆi+bˆj . Find the radius of curvature of the trajectory of the particle at (i) point of projection (ii) highest point .
View SolutionA ball is projected from a point in a horizontal plane so as to strike a vertical wall at right angle A.after rebounding from the wall it strikes the horizontal plane once and returns to the point of projection just before second collision at horizontal surface. Find co-efficient of restitution for the two collisions, assuming it to be same for both the collision.
View SolutionA particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
View SolutionA particle is projected with velocity u at an angle α from a point P on a horizontal plane strikes the plane at Q. The average velocity of the particle for its journey from P to Q is-
View Solution
