A stone is projected from the pont of a ground in such a direction so as to hit a bird on the top of a telegraph post of height h and then attain the maximum height 2h above the ground. If at the instnat of projection , the brid were to fly away horizontally with a unifrom speed , find the ratio between the horizontal velcoities of the bird and the stone , if stone still hits the bird while descending .
vucosθ=2√2+1
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - NUMERICAL EXERCISE (LEVEL -2)
17 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
A stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending.
View SolutionA stone is projected from the ground in such a direction so as to hit a bird on the top of a telegraph post of height h and attains the maximum height of 2h above the ground. If at the insatant of projection, the bird were to fly away horizontally with a uniform speed, find the ratio between the horizontal velocity of bird and the horizontal component of velocity of stone, if the stone hits the bird while descending.
View Solution
Knowledge Check
A stone is projected at an angle α to the horizontal from the top of a tower of height 3h If the stone reaches a maximum height h above the tower, then calculate the distance from the foot of the tower where particle strikes the foot of the where particle strikes the ground.
A6htanαB6hcotαChtanαDhcotαIf T be the total time of flight and H be the maximum height attained by a stone from the point of projection, then H/T will be ( u=projection velocity and θ=projection angle )
A(1/2)sinθB(1/4)usinθCusinθD2u sinθParticle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
AT2g2BT2g4CT2g8DT2g5
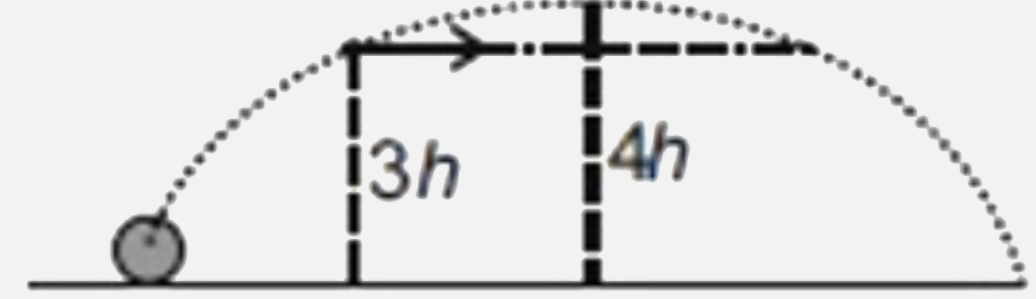
A stone is projected from a point on the ground in such a way so as to hit a bird at height 3h and could attain a maximum height 4h above the ground. If at the instant of projection, the bird flies away horizontally with speed 10ms−1 and the stone still hits the bird while descending, then the horizontal velocity of stone is
View SolutionA stone is projected at an angle α to the horizontal from the top of a tower of height 3h. If the stone reaches a maximum height 'h', above the tower, show that it reaches the ground at a distance 6h cot α from the foot of the lower.
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View Solution
A stone projected at an angle of 60∘ from the ground level strikes at an angle of 30∘ on the roof of a building of height h. Then the speed of projection of the stone is:
View SolutionA ball is thrown upwards with a speed u from a height h above the ground.The time taken by the ball to hit the ground is
View Solution
