To a man walking at the rate of 3 kmlh the rain appears to fall vertically. When he increases his speed to 6 kmlh it appears to meet him at an angle of 45° with vertical. Find the angle made by the velocity of rain with the vertical and its value.Solution in Telugu
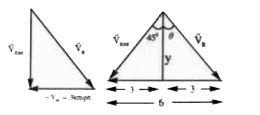
From the diagram tan45∘=3y………..(i)
and tanθ=3y……(2)
From (1) and (2) θ=45∘ and
∴sin45∘=3VR,1√2=3VR
VR=3√2 kmph
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola .
View SolutionWhat is the acceleration of a projectile at the top of its trajectory ?
View SolutionA particle ‘P is moving in a circle of radius "r" with uniform speed v. AB is the diameter of circle and 'C' is the centre. The angular velocity of P about A and C are in the ratio.
View SolutionGive two examples of the motion of big objects where the object can be treated as a particle and where it cannot be?
View SolutionTo a man walking at the rate of 3km/h the rain appear to fall vertically downwards. When he increases his speed 6km/h it appears to meet him at an angle of 45∘ with vertical. Find the speed of rain.
View SolutionRain appears to fall vertically to a man walking at 3kmh^(-1) , but when he changes his speed to double, the rain appears to fall at 45^@ with vertical. Study the following statements and find which of them are correct. i. Velocity of rain is 2 (sqrt3) kmh^(-1) . ii. The angle of fall of rain (with vertical) is theta = tan^(-1)(1/(sqrt2)). iii. The angle of fall of rain (with vertical) is theta = sin^(-1) (1/(sqrt2)) . iv. Velocity of rain is 3(sqrt2)kmh^(-1) .
View SolutionTo a man walking at 5kmph rain appears to fall vertically, and when he doubles his speed it appears to make an angle of 30∘ with the vertical. Find the actual velocity of the rain. In what direction will rain appear to fall if the man suddenly turns around when his speed is 5 kmph?
View SolutionTo a man walking due east at the rate of 2kmh^(-1) , rain appears to fall vertically. When he increases his speed to 4kmh^(-1) , its appears to meet him at an angle of 45^(@) . Find the real direction and speed of rain.
View SolutionWhen it is raining vertically down, to a man walking on road the velocity of rain appears to be 1.5 times his velocity. To protect himself from rain he should hold the umbrella at an angle θ to vertical. Then tanθ=
View SolutionTo a man walking at the rate of 3 km/h the rain appears to fall vertically. When he increases his speed 106 km/h it appears to meet him ar an angle of 450 with vertical. Find the angle made by the velocity of rain with the vertical and its value.
View SolutionTo a man walking at the rate of 3km/h the tain appears to fall vertically. When he increases his speed to 6km/h it appears to meet him at an angle of 45∘ with vertical. Find the angle made by the velocity of rain with the vertical and its value.
View SolutionRain drops appear to be falling at an angle with the vertical to a walking man why ?
View SolutionA man standing still finds rain pouring at an angle 30∘with vertical , when he starts walking forward at a speed of 4 kmph it appears to him that rain pours vertically down . When he runs at riple the speed, what is the angle at which rain appears to pour?
View SolutionTo a man walking at the rate of 3km/h the rain appear to fall vertically downwards. When he increases his speed 6km/h it appears to meet him at an angle of 45∘ with vertically. Find the speed of rain.
View SolutionTo a man walking at the rate of 3 km/h the rain appears to fall vertically. When he increases his speed to 6km/h it appears to meet him at an angle of 450 with vertical. Find the angle made by the velocity of rain with the vertical and its value.
View Solution
