A double slit interference pattern is produced on a screen, as shown in the figure, using momochromatic light of wavelength 500 nm. Point P is the location of the central bright fringe, that is produced when light waves arrive in phase without any path difference. A choice of the three strips A, B and C of transparent materials with different thickness and refractive indices is available, as shown in the table. These are placed over one or both of the slits, singularly or in conjunction causing the interference pattern to be shifted across the screen from the original pattern. In the Column - I, how the strips have been placed, is mentioned whereas in the Column-II, order of the fringe at point P on the screen that will be produced due to the placement of the strip(s), is shown. Correctly match both the column.
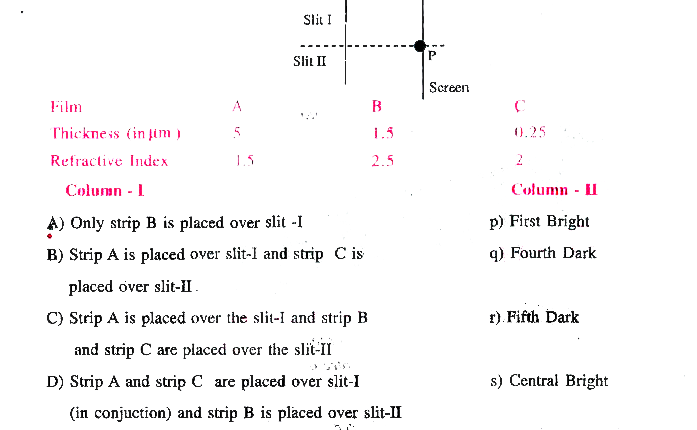
The correct Answer is:A-r; B-r; C-s; D-p
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Level - II (straight objective Type Questions) Integer Type Questions1videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET Exercise - II DIFFRACTION (Level - I (Main) (Straight objective Type questions)10videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Linked Comprehension type questions6videos
WAVE OPTICS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)81videos
WAVE MOTION AND SOUND
- BOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)15videos
WAVES
Similar Questions
In YDSE, the central bright fringe produced by light of wavelength 5600Å shifts to the position of 5th bright fringe when a thin transparent film of refractive index 1.28 is introduced in the path of light from one of the two slits. Find the thickness of the film.
View SolutionIn a double slit experiment, at a certain point on the screen the path difference between the two interfering waves is 13rd of a wavelength. The ratio of the intensity of light at that point to that at the centre of a bright fringe is:
View Solution
Knowledge Check
- Question 1 - Select One or More
Using monochromatic light of wavelength λ in Young's double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of _____.
A112πradB212πradC13πradD21πrad - Question 2 - Select One
In the interference pattern obtained in a biprism experiment, 5th order bright fringe is obtained at a point on the screen, when monochromatic light of wavelength 6000 Å is used. What is the order of the bright fringe produced at the samme point, if the light of wavelength 5000 Å is used?
An=3Bn=4Cn=6Dn=10 - Question 3 - Select One
Young's double slit experiment is being performed with a light of wavelength 6000 Å. It is given that the path difference at the central bright fringe is zero, then what is the path difference between the light coming from different slits at the fourth bright fringe?
A2.4×10−6mB1.2×10−6mC10−6mD0.5×10−6m
Laser light of wave length 600 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 8mm. A second light produces an interference pattern in which the fringes are separated by 12 mm. Calculate the wavelength of the second light.
View SolutionThe slits in Young's double slit experiment are illuminated by light of wavelength 6000Å. If the path difference at the central bright fringe is zero, what is the path difference for light from the slits at the fourth bright fringe?
View SolutionThe slits in Young's double slit experiment are illuminated by light of wavelength 6000 Ã…. If the path difference at the central bright fright fringe is zero, what is the path difference for light from the slits at the fourth bright frings?
View SolutionIn a double slit experiment, at a certain point on the screen the path difference between the two interfering waves is 13rd of a wavelength. The ratio of the intensity of light at that point to that at the centre of a bright fringe is:
View SolutionIn a double slit experiment, at a certain point on the screen the path difference between the two interfering waves is 13 rd of a wavelength. The ratio of the intensity of light at that point to that at the centre of a bright fringe is:
View Solution

