A unform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A . What is the torque on the loop in the different cases shown in the fig ? What is the force on each case? Which case corresponds to stable equilibrium ?
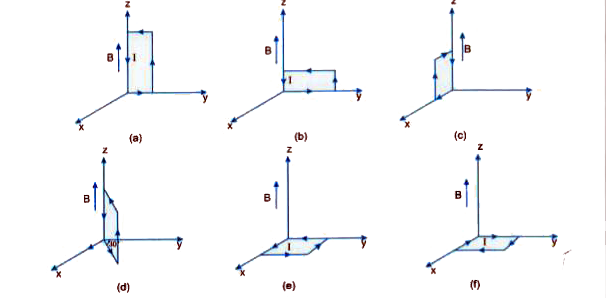
Here , length of loop breadth of loop b = 5 cm = 0.05 m and current
(a) Torque on the loop,
is pointing along x-axis]
The torque acts along - y direction . Force will act on the sides of the loop which are perpendicular to the magnetic field i.e., on the sides of the lenght, b each.
Therefore, force on these two sides = (along x-axis)
As two forces are equal and opposite hence net force on the loop is zero.
(b) Torque on the loop,
The force will act with equal magnitude on the sides which are perpendicular to hte magnetic field (on the sides of length l each). Hence Force on each of these two sides (along x - axis)
As two forces are equal in magntiude but mutually opposite in directions, hence net force on the loop is zero.
(c) Torque on the loop and forces on the sides are equal to the answers given in (a) but the direction of forces is along y - axis. Net force is even now zero.
(d) Torque on the loop and force forces on the sides are equal in magnitude as those in case (a). However, now the force is in a direction to the y-axis.
(e) and (f) , There is no side parallel to hte magnetic field around which loop can rotate, the torque is zero. Net force on the loop is zero.
Case (e) represents stable equilibrium because and the area vector is a parallel to hte magentic field . However , case (f) represents unstable equilibrium because the area vector is antiparallel to the magnetic field when the current flows through the loop.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - CASE BASED/SOURCE-BASED INTEGRATED QUESTIONS
18 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - MULTIPLE CHOICE QUESTIONS
35 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SELF ASSESSMENT TEST (SECTION D)
1 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
A uniform magnetic field of 3000G is established along the positive z-direction. A rectangular loop of sides 10cm and 5cm carries a current 12A. What is the torque on the loop in the different cases shown in the figure. What is the force on each case? Which case corresponds to stable equilibrium?

View SolutionA uniform magnetic field of 3000G is established along the positive z-direction. A rectangular loop of sides 10cm and 5cm carries a current 12A. What is the torque on the loop in the different cases shown in the figure. What is the force on each case? Which case corresponds to stable equilibrium?

View Solution
Knowledge Check
A uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
 AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4NmA uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
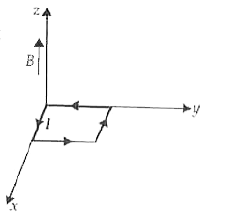 AzeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AzeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4NmA uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
 AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
A uniform magnetic field B of 0.3 T is along the positive Z-direction. A rectangular loop (abcd) of sides 10 cm × 5 cm carries a current I of 12 A. Out of the following different orientations which one corresponds to stable equilibrium?
View SolutionA rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnitude 0.20 T exists parallel to the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
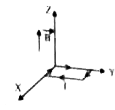
View SolutionA uniformi magnetic field of 3 T is established along the positive Z-direction. A rectangular loop in XY plane of sides 10 cm and 5 cm carries a current of 11 A as shown The torque on the loop is:
View SolutionA uniform magnetic field B of0.3 T is along the positive Z-direction. A rectangular loop (abed) of sides 10cm×5cm carries a current I of 12 A. Out of the following different orientations which one corresponds to stable equilibrium?
View SolutionA rectangular loop of sides 20cm and 10cm carries a current of 5.0A. A uniform magnetic field of magnitude 2T exists parallel to the longer side of the loop. The torque acting on the loop is
View Solution
