A beam of well collimated cathode rays travelling with a speed of 5 xx

A beam of well collimated cathode rays travelling with a speed of $5 \times 10^{6} m s^{- 1}$ enter a region of mutually perpendicular electric and magnetic fields and emerge undeviated from this region. If $| B | = 0.02 t$ , the magnitude of the electric field is
A $10^{5} V m^{- 1}$
B $2.5 \times 10^{8} V m^{- 1}$
C $1.25 \times 10^{10} V m^{- 1}$
D $2 \times 10^{3} V m^{- 1}$
A charged particle with a velocity $2 \times 10^{3} m s^{- 1}$ passes undeflected through electric field and magnetic fields in mutually perpendicular directions. The magnetic field is 1.5 t. the magnitude of electric field will be
A $1.5 \times 10^{3} N C^{- 1}$
B $2 \times 10^{3} N C^{- 1}$
C $3 \times 10^{3} N C^{- 1}$
D $1.33 \times 1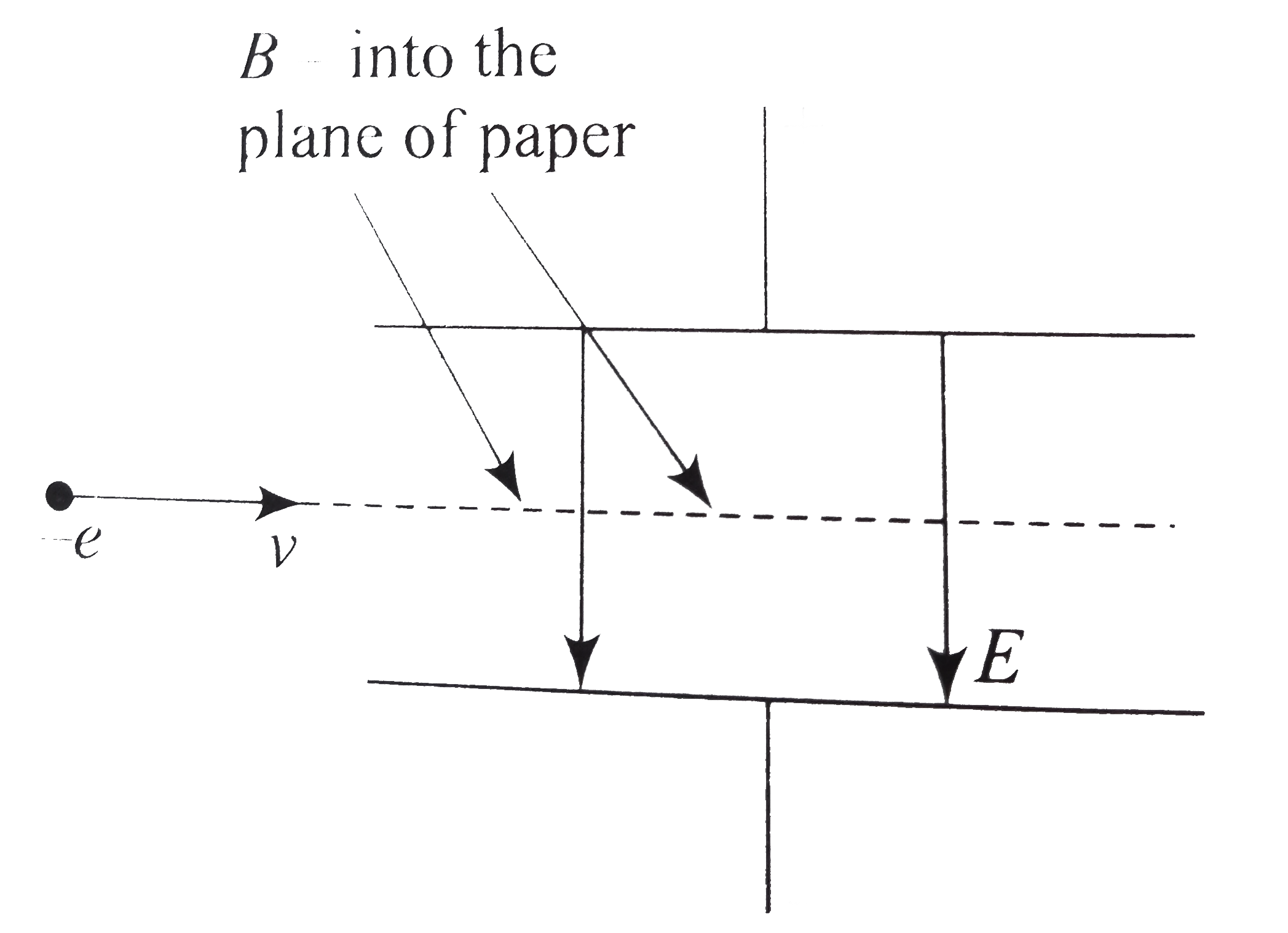0^{3} N C^{- 1}$
Electrons taveling at a velocity of $2.4 \times 10^{6} m s^{- 1}$ enter a region of crossed electric and magnetic fields as shoen in Fig. If the electric field is $3.0 \times 10^{6}$ Vm and the flux density of the magnetic field is 1.5 T, the electrons upon entering the region of the crossed fields will
Acontinue to travel undeflected in their original derection.
Bbe deflected upward in the plane of the diagram
Cbe deflected upward on the plane of the diagram
Dnone of the above

A beam of well collimated cathode rays travelling with a speed of $5 \times 10^{- 6} m s^{- 1}$ enters a region of mutually perpendicular electric and magnetic fields and emerge undeviated from the region if $∣ ∣ \to B ∣ ∣ = 0.02 T$ . The magnitude of the electric field is