An electron enters a region where magnetic field (B) and electric field (E ) are mutually perpendicular, then
it will always move in the direction of B
it will always move in the direction of E
it always possess circular motion
it can go undeflected also
The correct Answer is:d
To solve the problem, we need to analyze the motion of an electron in a region where the magnetic field (B) and electric field (E) are mutually perpendicular. We will determine under what conditions the electron can move undeflected.
1. Understanding the Forces:
- When a charged particle (like an electron) moves in an electric field (E) and a magnetic field (B), it experiences forces due to both fields.
- The force due to the electric field (F_E) is given by:
FE=qE
where q is the charge of the electron (which is negative) and E is the electric field strength.
2. Magnetic Force:
- The force due to the magnetic field (F_B) on a moving charge is given by:
FB=q(v×B)
where v is the velocity of the electron and B is the magnetic field.
3. Condition for Undeflected Motion:
- For the electron to move undeflected, the net force acting on it must be zero. This means that the electric force must equal the magnetic force in magnitude but opposite in direction:
FE+FB=0⟹FE=−FB
- Therefore, we can write:
qE=q(v×B)
- Since q is the same for both forces, we can cancel q (noting that q is negative for an electron):
E=vB
4. Direction of Fields and Velocity:
- For the forces to balance, the velocity vector (v) must be perpendicular to both the electric field (E) and the magnetic field (B).
- If E is in the negative z-direction and B is in the positive y-direction, then the velocity must be in the positive x-direction (or any direction that maintains the perpendicularity).
5. Conclusion:
- If the conditions are met (i.e., E=vB and all vectors are mutually perpendicular), the electron can move undeflected through the region where both fields exist.
Final Answer:
The electron can go undeflected if the electric and magnetic forces balance each other.
- When a charged particle (like an electron) moves in an electric field (E) and a magnetic field (B), it experiences forces due to both fields.
- The force due to the electric field (F_E) is given by:
FE=qE
where q is the charge of the electron (which is negative) and E is the electric field strength.
- The force due to the magnetic field (F_B) on a moving charge is given by:
FB=q(v×B)
where v is the velocity of the electron and B is the magnetic field.
- For the electron to move undeflected, the net force acting on it must be zero. This means that the electric force must equal the magnetic force in magnitude but opposite in direction:
FE+FB=0⟹FE=−FB
- Therefore, we can write:
qE=q(v×B)
- Since q is the same for both forces, we can cancel q (noting that q is negative for an electron):
E=vB
- For the forces to balance, the velocity vector (v) must be perpendicular to both the electric field (E) and the magnetic field (B).
- If E is in the negative z-direction and B is in the positive y-direction, then the velocity must be in the positive x-direction (or any direction that maintains the perpendicularity).
- If the conditions are met (i.e., E=vB and all vectors are mutually perpendicular), the electron can move undeflected through the region where both fields exist.
The electron can go undeflected if the electric and magnetic forces balance each other.
Similar Questions
A charged particle is at rest in the region where magnetic field and electric field are parallel. The particle will move in a
View SolutionA neutron, a proton, an electron and an α−particle enter a region of uniform magnetic field with equal velocities. The magnetic field is perpendicular to the paper and directed into it. The tracks of particles are labeled in Fig. 1.132. The neutron follows the track

View Solution
Knowledge Check
A moving electron enters a uniform and perpendicular magnetic field. Inside the magnetic field, the electron travels along :
Aa straight lineBa parabolaCa circleDa hyperbola
An electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionAn electron enters a region of space in which there exists an electric field 'E' and magnetic field 'B'. If the electron continues to move in the same direction with same velocity as before, the NOT possible case among the following is
View SolutionA moving electron enters a uniform and perpendicular magnetic field. Inside the magnetic field, the electron travels along :
View SolutionA proton of mass m and charge q enters a region of uniform magnetic field of a magnitude B with a velocity v directed perpendicular to the magnetic field. It moves in a circular path and leaves the magnetic field after completing a quarter of a circle. The time spent by the proton inside the magnetic field is proportional to:
View SolutionA charge particle is projected in a region of magnetic field and electric field if mass if mass of charged particle is m a its speed charges from V0 to 2V0[WE= work done by electric field WB= work done by magnetic field] which statement is incorrect.?
View SolutionAn electron is moving through a field. It is moving (i) opposite an electric field (ii) perpendicular to a magnetic field as shown. For each situation the de - Broglie wave length of electron
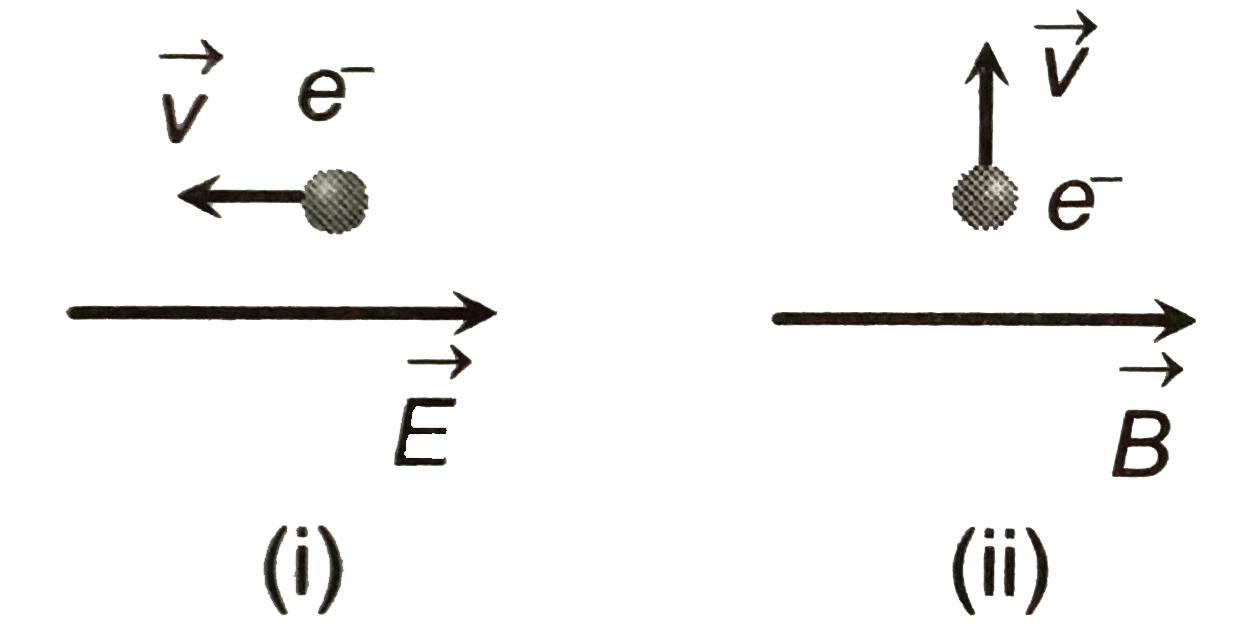
View SolutionIn a certain region of space electric field E and magnetic field B are perpendicular to each other and an electron enters region perpendicular to the direction of B and E both and moves undeflected, then velocity of electron is
(a) |E||B| (b) E×B (c) |B||E| (d) E.B
View Solution
