Two identical circular loops, P and Q, each of radius r and carrying currents I and 2 I respectively are lying in parallel planes such that they have a common axis. The direction of current in both the loops in clockwise as seen from O, which is euqidistant from both loops. Find the magnitude of the net magnetic field at point O.

The point O lies at the axial line of both the current carrying loops at a distance x = r from centre of either loop.
∴ Magnetic field due to coil P, BP=μ0INr22[r2+r2]3/2=μ0IN4√2r along QP
and magnetic field due to coil Q, BQ=μ0(2I)Nr22[r2+r3]3/2=μ0IN2√2r along PQ
As BPandBQ are in mutually opposite directions, hence net magnetic field at point Q
B=BQ−BP=μ0IN4√2r along PQ
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-I
33 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - VERY SHORT ANSWER QUESTIONS
39 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
Two identical circular loops, P and Q each of radius r and carrying currents I and 2I respectively are lying in parallel planes such that they have a common axis. Their centres are distance 2r apart. The direction of current in both the loops is clockwise as seen from O which is equidistant from both the loops. Find the magnitude of the net magnetic field at point O.

View SolutionTwo identical circular loops, P and Q each of radius r and carrying currents I and 2I respectively are lying in parallel planes such that they have a common axis. Their centres are distance 2r apart. The direction of current in both the loops is clockwise as seen from O which is equidistant from both the loops. Find the magnitude of the net magnetic field at point O.

View Solution
Knowledge Check
A circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.BzeroCinversely proportional to r.Ddirectly proportional to I.A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is parallel to the plane of the loop. The magnetic torque acting on the loop is-
AirBB2πriBCzeroDπr2iB
Two identical circular loops P and Q carrying equal currents are placed such that their geometrical axis are perpendicular to each other as shown in figure. And the direction of current appear’s anticlockwise as seen from point O which is equidistant from loop P and Q. Find the magnitude and direction of the net magnetic field produced at the p oint O.
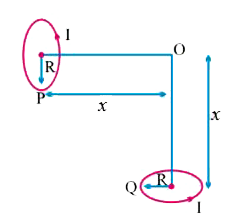
tanθ=B2B1=1,θ=π/4.
View SolutionTwo identical loops P and Q each of radius 5cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to 3A and 4A respectively.
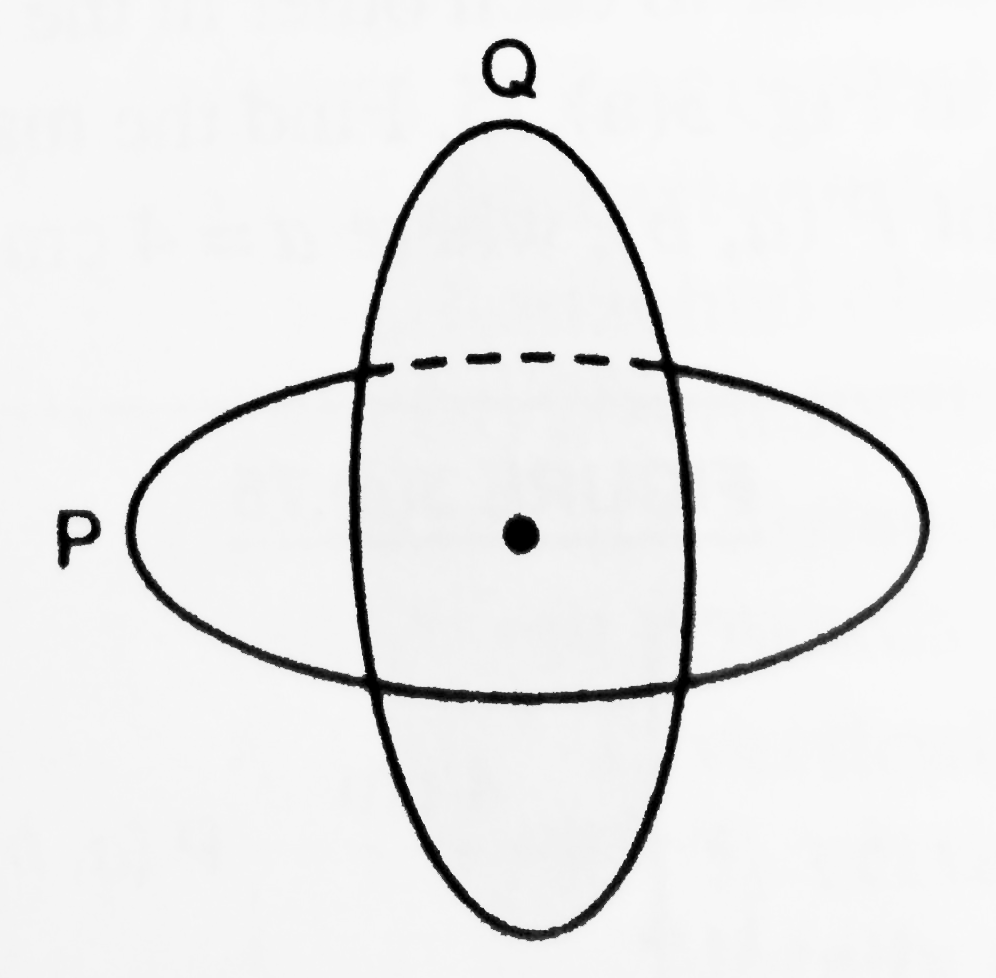
View SolutionTwo identical loops P and Q each of radius 5cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to 3A and 4A respectively.

View SolutionWhat is the magnetic moment of a circular loop of radius R carrying current I clockwise?
View SolutionA circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .
View SolutionA circular loop of area 1cm2 carrying a current of 10A is placed in a magnetic field of 2Tˆi. The loop is in xy plane with current in clockwise direction . Fing the torque on the loop
View Solution
