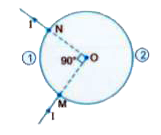
A current I enters a uniform circular loop of radius R at point M and flows out at N as shown in the Fig. Obtain the net magnetic field at the centre O of the loop.
The net magnet field at centre O of the loop is vector sum of fields due to two current segments 1 and 2 carrying currents I1andI2 and having resistance R1andR2 respectively. If V be the potential difference between M and N , then V=I1R1=I2R2
If R0 be the total resistance of entire loop than R1=90∘360∘R0=R04andR2=R0−R1 and R0−R04=3R04
⇒I2=I1R1R2=l1(R0/4)(3R0/4)=l13
∴ Field −→B1 due to current segment (1), −→B1=μ0I12R⋅14⊗
and field −→B2 due to current segment (2), −→B2=μ0I22R⋅34⊙=μ02R⋅li3⋅34⊙
⇒−→B2=μ0I12R⋅14⊙
∴ Net magnetic field at 0, →B=−→B1+−→B2=μ0I18R⊗+μ0I18R⊙=→0
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-I
33 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - VERY SHORT ANSWER QUESTIONS
39 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
Knowledge Check
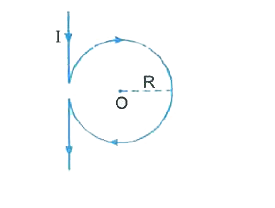
A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
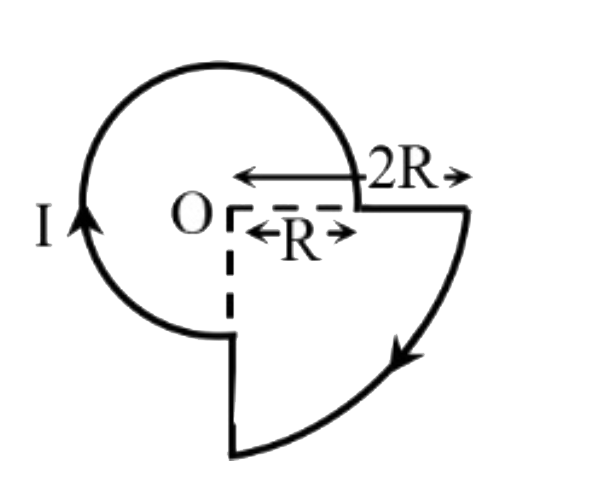
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)A current I flows through a long straight conductor which is bent into a circular loop of radius R in the middle as shown in the figure .
The magnitude of the net magnetic field at point O will beAZeroBμ0I2R(1+π)Cμ0I4πRDμ0I2R(1−1π)
A current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
View SolutionA circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View Solution