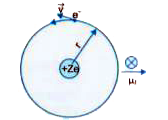
An electron of mass $m_{e}$ , revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence, prove that the magnetic moment associated with it is expressed as $\to μ = - \frac{e}{2 m_{e}} \to L$ , where $\to L$ is the orbital angular momentum of the electron. Give the significance of negative sign.

Text Solution

Verified by Experts

We know that a revolving electron constitutes an electric current given by
$I = \frac{e}{T} = \frac{e v}{2 π r}$
where $T = \frac{2 π r}{v}$ = peroid of revolution of electron revolving in a circular orbit of radius r with a speed v.
$∴$ Magnetic moment $(μ_{l})$ associated with this circulating current,
$μ_{l} = I \cdot A = \frac{e v}{2 π r} \cdot π r^{2} = \frac{e v r}{2}$
As an electron revolving is an anticlockwise direction is equivalent to current in clockwise direction, hence in accordance with right hand rule the magnetic moment is in a direction perpendicular to plane of paper (or plane of orbit) directed inward.
The above relation may also bewritten as :
$μ_{l} = \frac{e v r m}{2 m} = \frac{e}{2 m} \cdot l$
and in vector notation, ${\to μ}_{l} = - \frac{e}{2 m} \cdot \to l,$ where $l = m v r$ = orbital angular momentum of the electron around the nucleus . The -ve sign applied here indicates that the angular momentum of the electorn is opposite in direction to the magnetic moment.

Updated on:21/07/2023