Two coplanar and concentric coils 1 and 2 have respectively the number of turns N1 and N2 and radii r1 and r2(r2>>r1). Deduce the expression for mutual inductance of this system.
Let us have two concentric coils of no. of turns N1 and N2 and radii r1 and r2(r2>>r1). Let a current I2 flows through the outer coil no 2. Then magnetic field at the common centre of coils.
B=μ0N2I22r2
Since r1<<r2 field may be considered to be uniform across entire coil no 1. Hence, total magnetic flux linked with inner coil is :
ϕ1=N1BA1=N1B(π21)=N1×μ0N2I22r2×πr21=μ0πN1N2r21l22r2
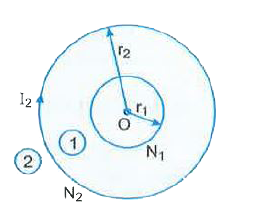
∴ Mutual inductance of the system M =ϕI2=μ0πN1N2r212r2
Topper's Solved these Questions
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION C
8 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
6 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- MAGNETISM AND MATTERBOOK - U-LIKE SERIESCHAPTER - MAGNETISM AND MATTEREXERCISE - SELF ASSESSMENT TEST (Section D)
1 Videos
Similar Questions
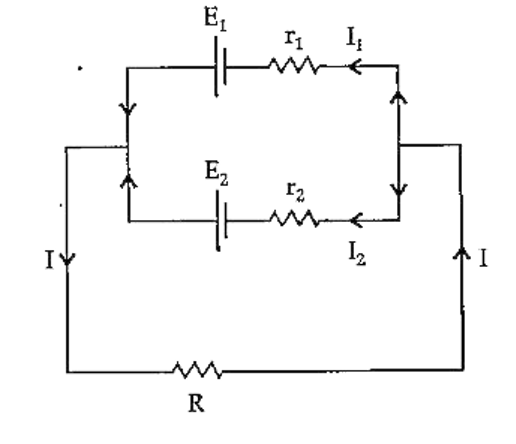
Two cells of emf E1 and E2 have internal resistance r1 and r2. Deduce an expression for equivalent emf of their parallel combination.
View SolutionTwo concentric spherical shells have masses m1andm2 and radii r1andr2(r2>r1). What is the force exerted by this system on a particle of mass m3. If it is placed at a distance r(r1<r<r2) from the centre ?
View Solution
Knowledge Check
Two soap bubbles A and B have radii r1andr2 respectively. If r1<r2 than the excess pressure inside
Abubbles A and B will be equalBbubbles A will be less than that in bubbles BCbubbles A will be greater than that in bubble BDbubbles A and B will be zero.The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1Two concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field on a mass m?
 AF=G(M1+M2)r2, for r<r1BF=G(M1+M2)(r2), for r<r2CF=GM2r2, for r1<r<r2DF=GM1r2, for r1<r<r2
AF=G(M1+M2)r2, for r<r1BF=G(M1+M2)(r2), for r<r2CF=GM2r2, for r1<r<r2DF=GM1r2, for r1<r<r2
Two concentric spherical shells have masses m1andm2 and radii r1andr2(r2>r1). What is the force exerted by this system on a particle of mass m3. If it is placed at a distance r(r1<r<r2) from the centre ?
View Solution(a) Explain the meaning of the term mutual inductance. Consider two concentric circular coils, one radius r1 and the other of radius r2(r1<r2) placed coaxially with centres coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
(b) A rectangular coil of area A, having number of turns N is rotated at 'f' revoluation per second in a uniform magnetic field B, the field being perpendicular to the coil. Prove that maximum emf induced in the coil is 2πfNBA.
View SolutionTwo concentric shells of masses M1 and M2 are having radii r1 and r2. Which of the following is the correct expression for the gravitational field at a distance r ?
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionA solenoid S1 is placed inside another solenoid S2 as shown in the fig. The radii of the inner and the outer solenoids are r1 and r2 respectively and the numbers of turns per unit length are n1 and n2 respectively. Consider a length I of each solenoid. Calculate the mutual inductance between them.

View Solution

