$(a)$ Explain the meaning of the term mutual inductance. Consider two concentric circular coils, one radius $r_{1}$ and the other of radius $r_{2} (r_{1} < r_{2})$ placed coaxially with centres coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
$(b)$ A rectangular coil of area $A$ , having number of turns $N$ is rotated at $' f'$ revoluation per second in a uniform magnetic field $B$ , the field being perpendicular to the coil. Prove that maximum emf induced in the coil is $2 π f N B A$ .

Video Solution

Text Solution

Verified by Experts

$(a)$ Mutual Inductance : When current flowing in one of two nearby coils is changed, the magnetic flux linked with the other coil changes , due to which an emf is induced in it (other coil). This phenomenon of electromagnetic induction. The coil, in which current is changed is called the primary coil and the coil in which emf is induced is called the secondary coil i.e., the mutual inductance between two coils is numerically equal to the effective flux linkage with secondary coil, when current flowing in primary coil is $1$ ampere .
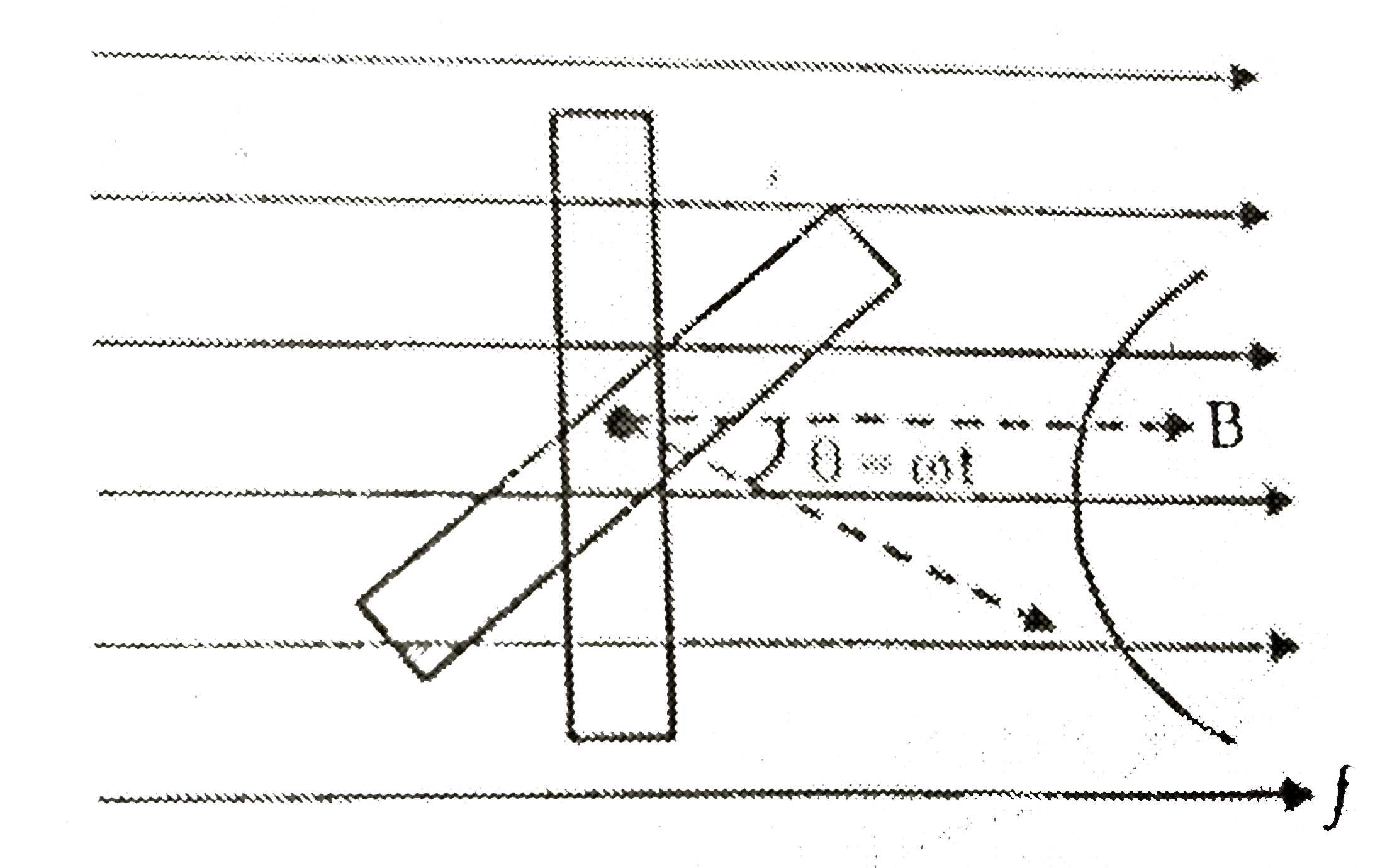
Mutual Inductance of Two Co-axial Solenoids : Consider two long-co-axial solenoids each of length $l$ with number of turns $N_{1}$ and $N_{2}$ wound one over the other. Number of turns per unit length in order (primary) solenoid, $n = \frac{N_{1}}{l}$ . If $I_{1}$ is the current flowing in primary solenoid, the magnetic field produced within the solenoid.
$B_{1} = \frac{μ_{0} N_{1} I_{1}}{l}$
The flux linked with each turn of inner solenoid coil is $ϕ_{2} = B_{1} A_{2}$ , where $A_{2}$ is the cross-sectional area inner solenoid. The total flux linkage with inner coil of $N_{2}$ -turns,
$φ_{2} = N_{2} ϕ_{2} = N_{2} B_{1} A_{2} = N_{2} (\frac{μ_{0} N_{1} I_{1}}{l}) A_{2} = \frac{μ_{0} N_{1} N_{2}}{l} A_{2} I_{1}$
By definition Mutual Inductance $M_{2} I = \frac{φ_{2}}{I_{1}} = \frac{μ_{0} N_{1} N_{2} A_{2}}{l}$ .
If $n_{1}$ is number of turns per unit length of outer solenoid and $r_{2}$ is radius of inner solenoid, the $M = μ_{0} n_{1} N_{2} π r_{22}$ .
$(b) (i)$ Suppose initially the plane of coil is perpendicular to the magnetic field $B$ . When coil rotates with angular speed $q$ , then after $t$ , the angle between magnetic field and normal to plane of coil is
$θ = ω t$
$∴$ At this instant magnetic flux linked with coil $ϕ = B A cos ω t$
If coil constants $N$ -turns, then emf induced in the coil
$ε = - N \frac{d ϕ}{d t} = - N \frac{d}{d t} (B A cos ω t)$
$∴$ For maximum value of emf $ε$ ,
$sin ω t = 1$
$∴$ Maximum emf induced, $ε_{max} = N B A ω$ .
$= 2 π f N B A$

Updated on:21/07/2023

Two concentric circular coils, one of small radius $r_{1}$ and the other of large radius $r_{2}$ such that $r_{1} < < r_{2}$ are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
A $\frac{μ_{0} π t r_{1}^{2}}{2 r_{2}}$
B $\frac{μ_{0} π t r_{2}^{2}}{2 r_{1}}$
C $\frac{μ_{0} π t r_{2}^{2}}{r_{1}}$
D $\frac{μ_{0} π t r_{1}^{2}}{r_{2}}$
The magnetic induction at the centre of a current carrying circular of coil radius $r$ , is
ADirectly proportional to $r$
BInversely proportional $r$
CDirectly proportional to $r$
DInversely proportional to $r$
A circular coil of radius r is placed in a uniform magnetic field B. The magnetic field is normal to the plane of the coil is rotated at an angular speed of $ω$ , about its own axis , then the induced emf in the coil is __

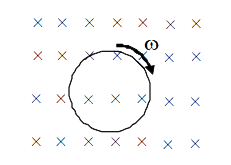A $\frac{B A ω}{2 π}$
B $B (2 π r) ω$
C0
Dnone of the above