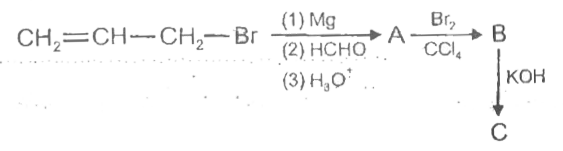
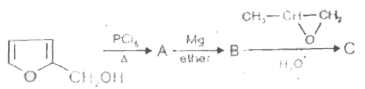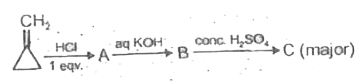In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
To find how many people liked product C only, we can use the principle of inclusion-exclusion and a Venn diagram to visualize the problem. Here’s the step-by-step solution:
Step 1: Define the Sets
Let:
- A = Set of people who liked product A
- B = Set of people who liked product B
- C = Set of people who liked product C
From the problem, we have:
- |A|=21
- |B|=26
- |C|=29
- |A∩B|=14
- |A∩C|=12
- |B∩C|=14
- |A∩B∩C|=8
Step 2: Calculate the Number of People Liking Each Pair of Products
To find the number of people who liked only two products, we can subtract those who liked all three products from the intersections.
1. People who liked both A and B but not C:
|A∩B|−|A∩B∩C|=14−8=6
2. People who liked both A and C but not B:
|A∩C|−|A∩B∩C|=12−8=4
3. People who liked both B and C but not A:
|B∩C|−|A∩B∩C|=14−8=6
Step 3: Calculate the Number of People Who Liked Only Product C
To find the number of people who liked only product C, we can use the total number of people who liked product C and subtract those who liked C along with A or B or both.
The total number of people who liked product C is given as 29. We need to subtract:
- Those who liked A and C (including those who liked all three): 4 (only A and C) + 8 (all three) = 12
- Those who liked B and C (including those who liked all three): 6 (only B and C) + 8 (all three) = 14
Thus, the number of people who liked only product C is:
|C|−(|A∩C|+|B∩C|−|A∩B∩C|)=29−(4+8+6)=29−18=11
Final Answer
The number of people who liked product C only is 11.
Let:
- A = Set of people who liked product A
- B = Set of people who liked product B
- C = Set of people who liked product C
- |A|=21
- |B|=26
- |C|=29
- |A∩B|=14
- |A∩C|=12
- |B∩C|=14
- |A∩B∩C|=8
To find the number of people who liked only two products, we can subtract those who liked all three products from the intersections.
|A∩B|−|A∩B∩C|=14−8=6
|A∩C|−|A∩B∩C|=12−8=4
|B∩C|−|A∩B∩C|=14−8=6
To find the number of people who liked only product C, we can use the total number of people who liked product C and subtract those who liked C along with A or B or both.
- Those who liked A and C (including those who liked all three): 4 (only A and C) + 8 (all three) = 12
- Those who liked B and C (including those who liked all three): 6 (only B and C) + 8 (all three) = 14
|C|−(|A∩C|+|B∩C|−|A∩B∩C|)=29−(4+8+6)=29−18=11
The number of people who liked product C only is 11.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - SETSEXERCISE - SOLVED EXAMPLES34videos
SETS
- BOOK - NCERT ENGLISHCHAPTER - SETSEXERCISE - EXERCISE 1.39videos
SETS
- BOOK - NCERT ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - EXERCISE 9.56videos
SEQUENCES AND SERIES
- BOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE 15.210videos
STATISTICS
Similar Questions
In a survery, it was found that 21 persons liked product A, 26 liked product B and 29 liked product C. If 14 persons liked products A and B, 12 liked products C and A, 13 persons liked products B and C and 8 liked all the three products then
(i) Find the number of persons who liked the product C only
(ii) The number of persons who like the products A and B but not CView Solution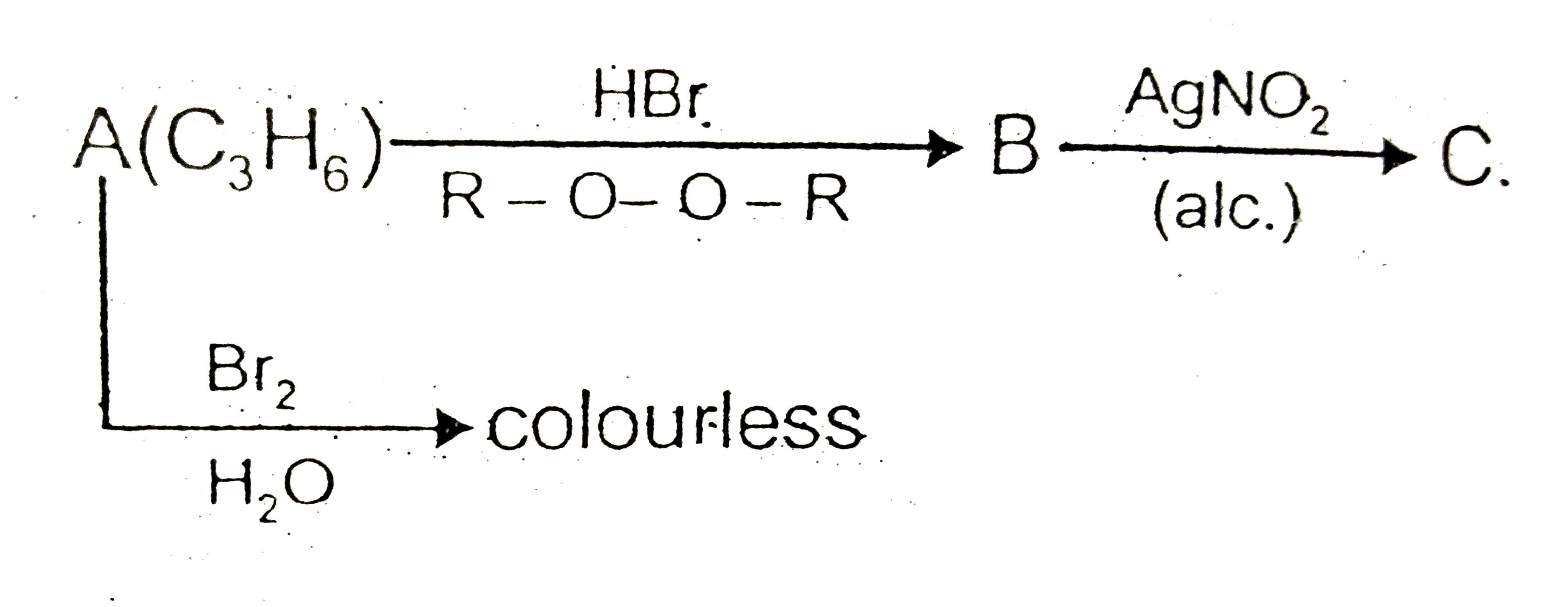
The product C isView Solution
Knowledge Check
- Question 1 - Select One or More
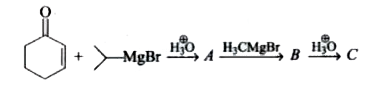
Product A and C are:A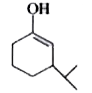 B
B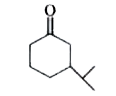 C
C D
D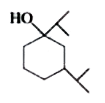



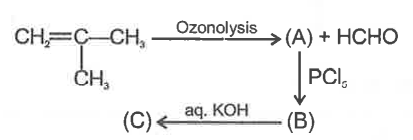 The product "C" is
The product "C" is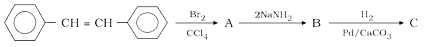 The product (C) is :
The product (C) is : . The product C is
. The product C is