In a survery, it was found that 21 persons liked product A, 26 liked product B and 29 liked product C. If 14 persons liked products A and B, 12 liked products C and A, 13 persons liked products B and C and 8 liked all the three products then
(i) Find the number of persons who liked the product C only
(ii) The number of persons who like the products A and B but not C
The correct Answer is:(i)12(ii)6
To solve the problem, we will use a Venn diagram to represent the relationships between the persons who liked products A, B, and C. Let's denote the number of persons who liked:
- Product A = 21
- Product B = 26
- Product C = 29
- Both A and B = 14
- Both A and C = 12
- Both B and C = 13
- All three products (A, B, and C) = 8
Step 1: Fill in the Venn Diagram
1. All three products (A, B, C): The number of persons who liked all three products is given as 8. We place this in the center where all three circles overlap.
2. A and B only: The number of persons who liked both A and B is 14. Since 8 liked all three products, the number who liked only A and B is:
(A∩B)−(A∩B∩C)=14−8=6
We place 6 in the section where only A and B overlap.
3. A and C only: The number of persons who liked both A and C is 12. Again, since 8 liked all three products, the number who liked only A and C is:
(A∩C)−(A∩B∩C)=12−8=4
We place 4 in the section where only A and C overlap.
4. B and C only: The number of persons who liked both B and C is 13. Therefore, the number who liked only B and C is:
(B∩C)−(A∩B∩C)=13−8=5
We place 5 in the section where only B and C overlap.
5. A only: The total number of persons who liked product A is 21. We have already accounted for 6 (A and B only), 4 (A and C only), and 8 (A, B, and C). Thus, the number who liked only A is:
A−(A∩B)−(A∩C)+(A∩B∩C)=21−6−4−8=3
We place 3 in the section for A only.
6. B only: The total number of persons who liked product B is 26. We have accounted for 6 (A and B only), 5 (B and C only), and 8 (A, B, and C). Thus, the number who liked only B is:
B−(A∩B)−(B∩C)+(A∩B∩C)=26−6−5−8=7
We place 7 in the section for B only.
7. C only: The total number of persons who liked product C is 29. We have accounted for 4 (A and C only), 5 (B and C only), and 8 (A, B, and C). Thus, the number who liked only C is:
C−(A∩C)−(B∩C)+(A∩B∩C)=29−4−5−8=12
We place 12 in the section for C only.
Summary of the Venn Diagram
- Only A: 3
- Only B: 7
- Only C: 12
- A and B only: 6
- A and C only: 4
- B and C only: 5
- A, B, and C: 8
Step 2: Answer the Questions
(i) Find the number of persons who liked product C only:
From our calculations, we found that the number of persons who liked only product C is 12.
(ii) The number of persons who like the products A and B but not C:
From our calculations, we found that the number of persons who liked both A and B but not C is 6.
Final Answers
(i) The number of persons who liked product C only is 12.
(ii) The number of persons who like products A and B but not C is 6.
- Product B = 26
- Product C = 29
- Both A and B = 14
- Both A and C = 12
- Both B and C = 13
- All three products (A, B, and C) = 8
(A∩B)−(A∩B∩C)=14−8=6
We place 6 in the section where only A and B overlap.
(A∩C)−(A∩B∩C)=12−8=4
We place 4 in the section where only A and C overlap.
(B∩C)−(A∩B∩C)=13−8=5
We place 5 in the section where only B and C overlap.
A−(A∩B)−(A∩C)+(A∩B∩C)=21−6−4−8=3
We place 3 in the section for A only.
B−(A∩B)−(B∩C)+(A∩B∩C)=26−6−5−8=7
We place 7 in the section for B only.
C−(A∩C)−(B∩C)+(A∩B∩C)=29−4−5−8=12
We place 12 in the section for C only.
- Only A: 3
- Only B: 7
- Only C: 12
- A and B only: 6
- A and C only: 4
- B and C only: 5
- A, B, and C: 8
From our calculations, we found that the number of persons who liked only product C is 12.
From our calculations, we found that the number of persons who liked both A and B but not C is 6.
(i) The number of persons who liked product C only is 12.
(ii) The number of persons who like products A and B but not C is 6.
Topper's Solved these Questions
Similar Questions
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
View SolutionIn a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked products C only?
View Solution
Knowledge Check
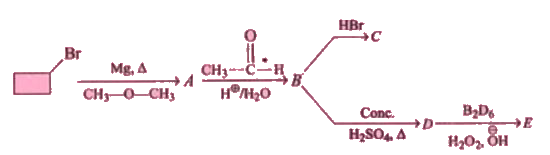
Find the major product 'C':A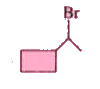 B
B C
C D
D
Identify the products A, B and C:

View SolutionIn a survey, 50 people like product A, 30 people like product B and 20 people like product C and 35 people like exactly two products. If 5 people like all the three products then number of people who do not like any product . [There are 100 people in survey]
View Solution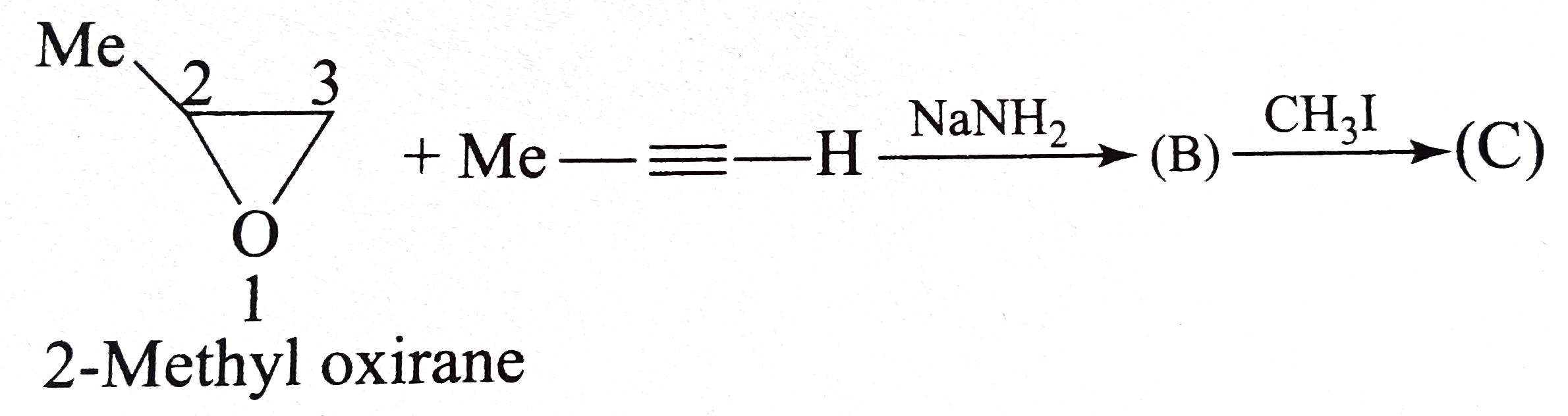
Give the products (B) and (C) in the above reaction.
View Solution
The product B and C are respectively:
View Solution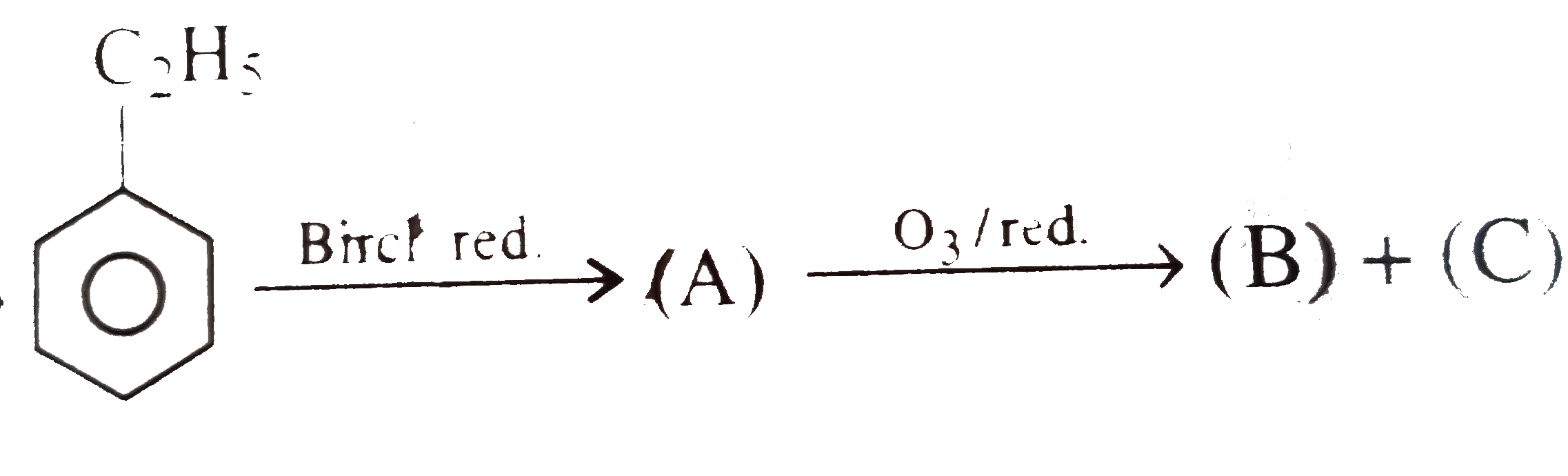
The product (B), and (C) are:
View Solution , Product B and C are respectively :
, Product B and C are respectively :
View Solution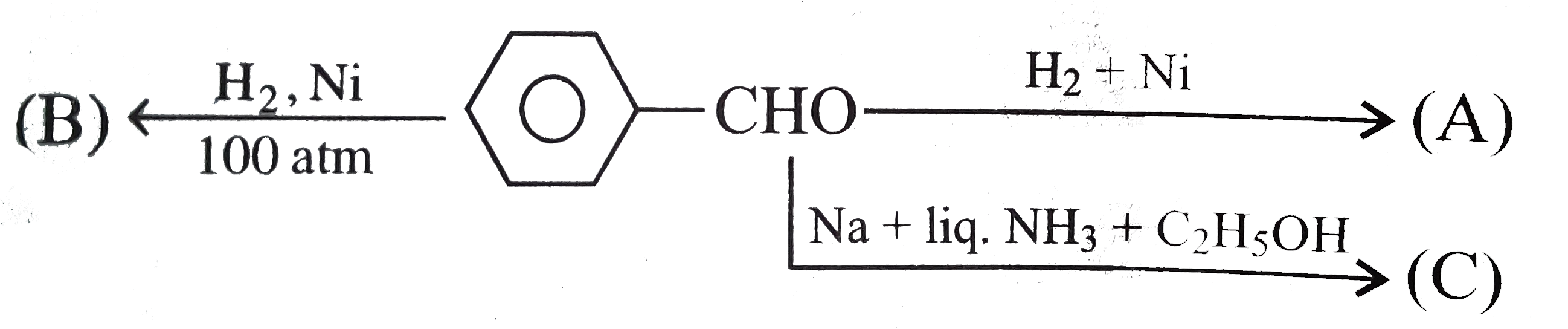
The products (A), (B), and (c ) are:
View Solution
