In a circle of diameter 40 cm. The length of a chord is 20 cm. Find the length of minor arc of the chord.
Diameter of the circle =40 cm
∴ Radius (r) of the circle = 402cm
=20cm
Let AB be a chord (length = 20cm) of the circle.
In △OAB,OA=OB = Radius of circle = 20cm
Also, AB=20cm
Thus, △OAB is an equilateral triangle.
∴θ=602=π3radian
We know that in a circle of radius r unit, if an arc of length I unit subtends an angle θ radian at the centre, then θ=1r
then, π3=arcAB20=arcAB=20π3 cm
Topper's Solved these Questions
Similar Questions
In a circle of diameter 60 cm the length of a chord is 30 cm. Find the length of the minor and major arcs of the chord.
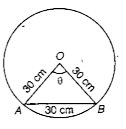
View SolutionA chord of a circle of diameter 30 cm is of length 15 cm. Find the length of mirror arc corresponding to this chord.
View SolutionTwo parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm, find the length of the other chord.
View SolutionThe radius of a circle is 15cm. Find the length of its longest chord.
View SolutionThe radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centres.
View SolutionThe radius of a circle is 13 cm and the length of one of its chords is 10 cm. Find the distance of the chord from the centre.
View Solution(i) Find the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13cm.
(ii) The length of a chord is 16 cm of a circle of diameter 2 cm. find the perpendicular distance of this chord from the centre of the circle.
View SolutionThe radius of a circle is 30 cm. find the length of an arc this circle, if the length of the chord of the arc is 30 cm.
View SolutionThe radius of a circle is 30 cm. find the length of an arc this circle, if the length of the chord of the arc is 30 cm.
View SolutionThe diameter and a chord of a circle have a common end point. If the lengt of the diameter is 20 cm and the length of the chord is 12 cm, how far is the chrod from the centre of the circle?
View Solution
