Question

The radius of a circle is 30 cm. find the length of an arc this circle,
if the length of the chord of the arc is 30 cm.

Explanation

To find the length of the arc of a circle given the radius and the length of the chord, we can follow these steps:

Step 1: Understand the given information
- The radius of the circle (r) = 30 cm
- The length of the chord (AB) = 30 cm

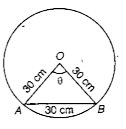
Step 2: Draw the circle and label the points
- Let O be the center of the circle.
- Let A and B be the endpoints of the chord.
- The triangle OAB is formed by the radius OA, OB, and the chord AB.

Step 3: Identify the triangle type
Since OA = OB = 30 cm (both are radii), and AB = 30 cm, triangle OAB is an equilateral triangle (all sides are equal).

Step 4: Calculate the angle θ
In an equilateral triangle, all angles are equal. Therefore, the angle θ at O (∠AOB) is:
\( \theta = 60^\circ \)

Step 5: Convert the angle from degrees to radians
To use the arc length formula, we need to convert θ from degrees to radians. The conversion formula is:
\( \text{radians} = \text{degrees} \times \frac{\pi}{180} \)
So,
\( \theta = 60^\circ \times \frac{\pi}{180} = \frac{\pi}{3} \text{ radians} \)

Step 6: Use the arc length formula
The formula for the length of an arc (l) is given by:
\( l = r \cdot \theta \)
Substituting the values we have:
\( l = 30 \cdot \frac{\pi}{3} \)

Step 7: Simplify the expression
Calculating the above expression:
\( l = 10\pi \text{ cm} \)

Final Answer
The length of the arc AB is \(10\pi\) cm.

---