Find the area of the region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}
Video Solution
Text Solution
Let us first sketch the region whose area is to be found out. This region is the intersection of the following regions.
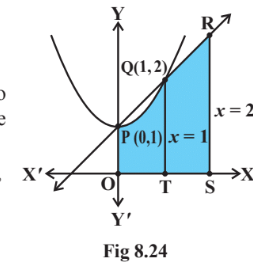
area of the region OTQPO + area of the region TSRQT
so required area is =∫10(x2+1)dx+∫21(x+1)dx
(x33+x)10+(x22+x)21
(13+1)+(4−32)
43+52=236sq unit
|
Topper's Solved these Questions
- APPLICATION OF INTEGRALSBOOK - NCERT ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Exercise 8.1
13 Videos
- APPLICATION OF INTEGRALSBOOK - NCERT ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.2
7 Videos
- APPLICATION OF INTEGRALSBOOK - NCERT ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - EXERCISE 8.2
7 Videos
- APPLICATION OF DERIVATIVESBOOK - NCERT ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - SOLVED EXAMPLES
51 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - NCERT ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE 5.7
17 Videos
Similar Questions
Find the area of the region {(x,y):x2+y2≤1≤x+y}.
View SolutionFind the area of the region {(x,y) :x2+y2≤4, x+y ≥2}
View SolutionFind the area of the region {(x,y) :x2+y2≤4, x+y ≥2}
View SolutionFind the area of the region {(x,y):x2+y2≤1≤x+y}
View SolutionUsing integration, find the area of the region
{(x,y):x2+y2≤1,x+y≥1,x≥0,y≥0}
View SolutionFind the area of the region {(x,y)/x2−x−1≤y≤−1}
View SolutionFind the area of region : {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}.
View SolutionFind the area of the region bounded by y =x2+1,y=x ,x=0 and y=2
View SolutionFind the area of the region bounded by the curves y=x2+2, y=x,x=0andx=3.
View SolutionFind the area of the region bounded by
y=ex and y = x between x = 0 and x = 1.
View Solution
