In a fig. 23.4 (a square), identify the following vectors: Coinitial ii. Equal Collinear but not equal
(i)Vectors a and d are coinitial because they have the same initial point.
(ii) Vectors b and d are equal because they have the same magnitude and direction.
(iii) Vectors a and c are collinear but not equal as they are parallel, their directions are not the same.
Vectors b and d are collinear and equal vectors as they are parallel and their directions are same.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - NCERT ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - MISCELLANEOUS EXERCISE
19 Videos
- VECTOR ALGEBRABOOK - NCERT ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise 10.5
7 Videos
- VECTOR ALGEBRABOOK - NCERT ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - EXERCISE 10.3
18 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - NCERT ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 11.3
14 Videos
Similar Questions
In a fig 23.4 (a square), identify the following vectors: i.Coinitial ii.Equal iii.Collinear but not equal
View SolutionIn the given figure, identify the following vectors :
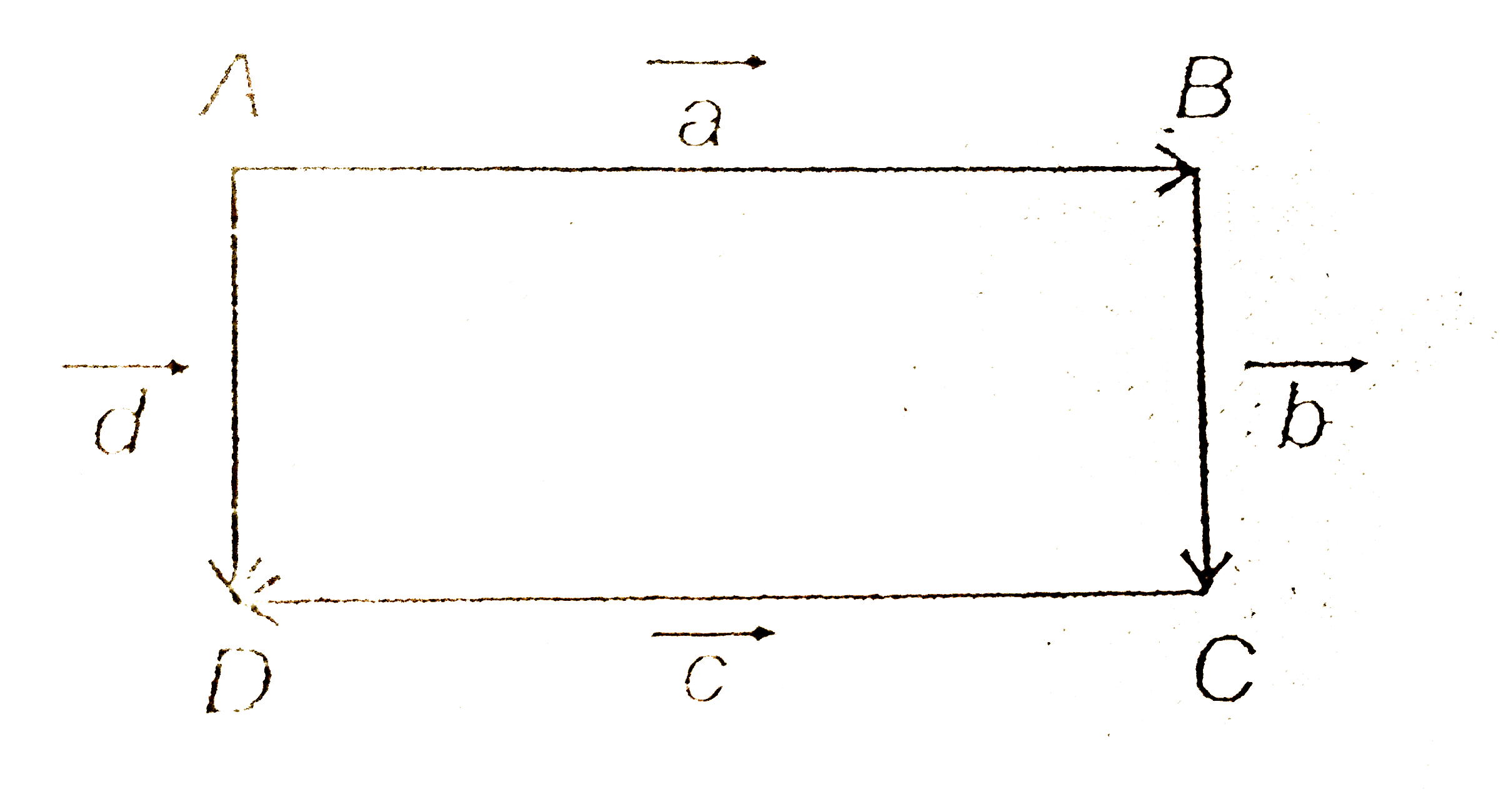
Coinitial
Equal
View SolutionIn the given figure identify the following vectors: equal
View SolutionIn the given figure identify the following vectors: collinear but not equal
View SolutionIn the given figure, vectors which are
Collinear
Equal
Collinear but not equal.

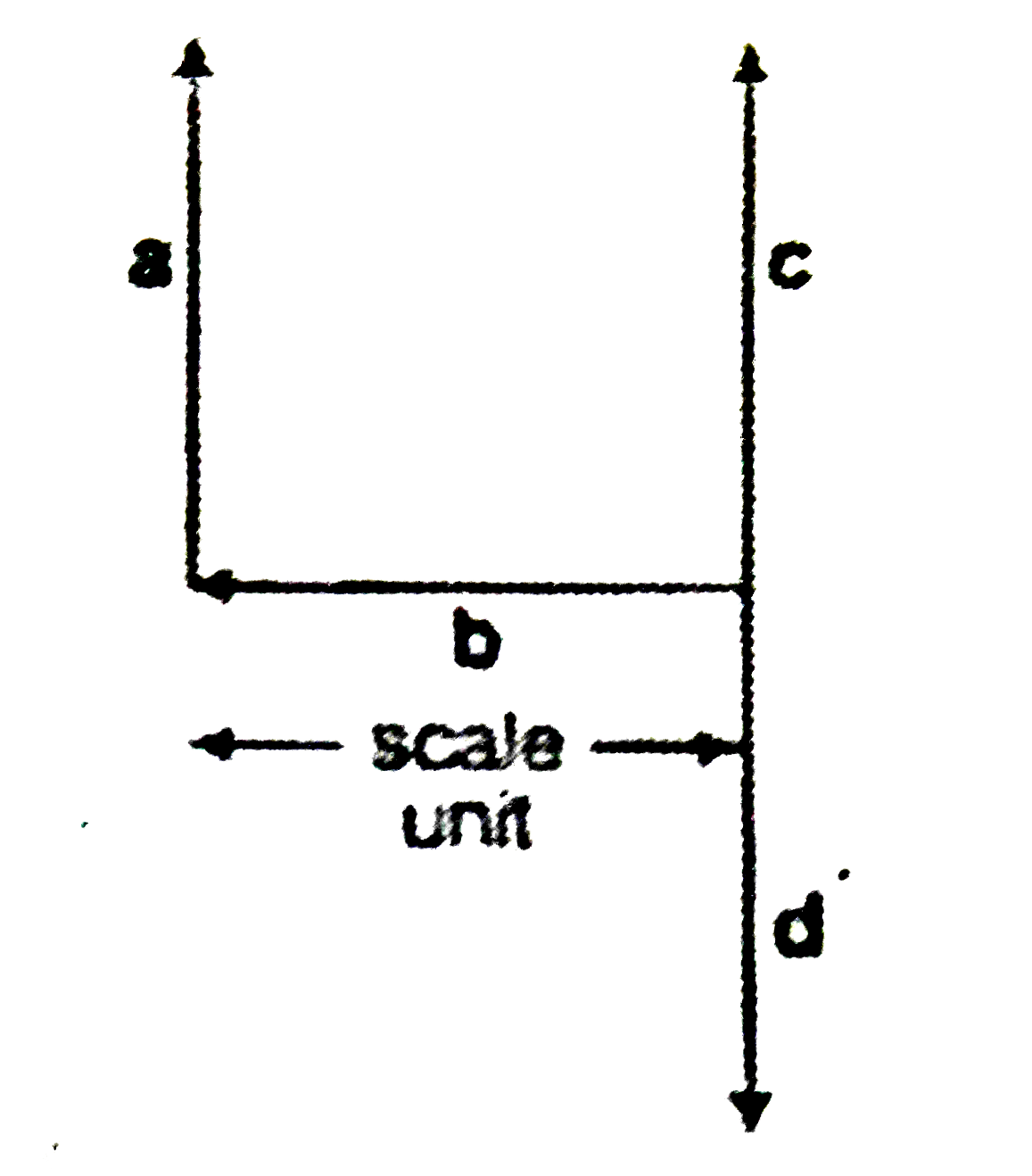
View SolutionIn the following figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial
(iv) collinear but not equal .
View SolutionIn Fig. ABCD is a regular hexagon, which vectors are: (i) Collinear (ii) Equal (iii) Coinitial (iv) Collinear but not equal
View SolutionIn the given figure, ABCDEF is a regular hexagon, which vectors are:
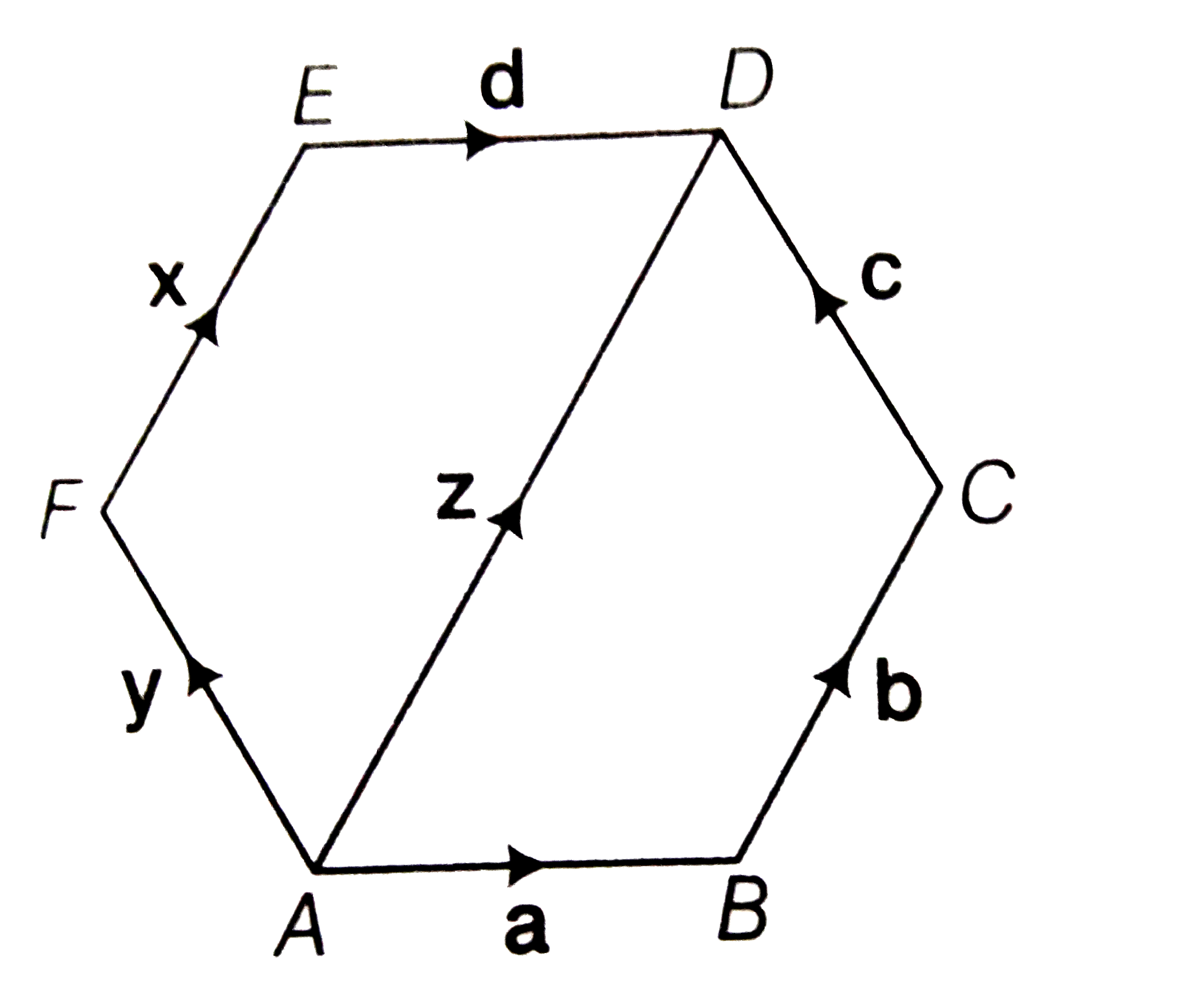
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
View SolutionIn fig 23.3, which of the vectors are: i.Collinear ii. Equal iii. Co-initial
View SolutionWhich of the following vector is equal as that of −−→1m
View Solution
