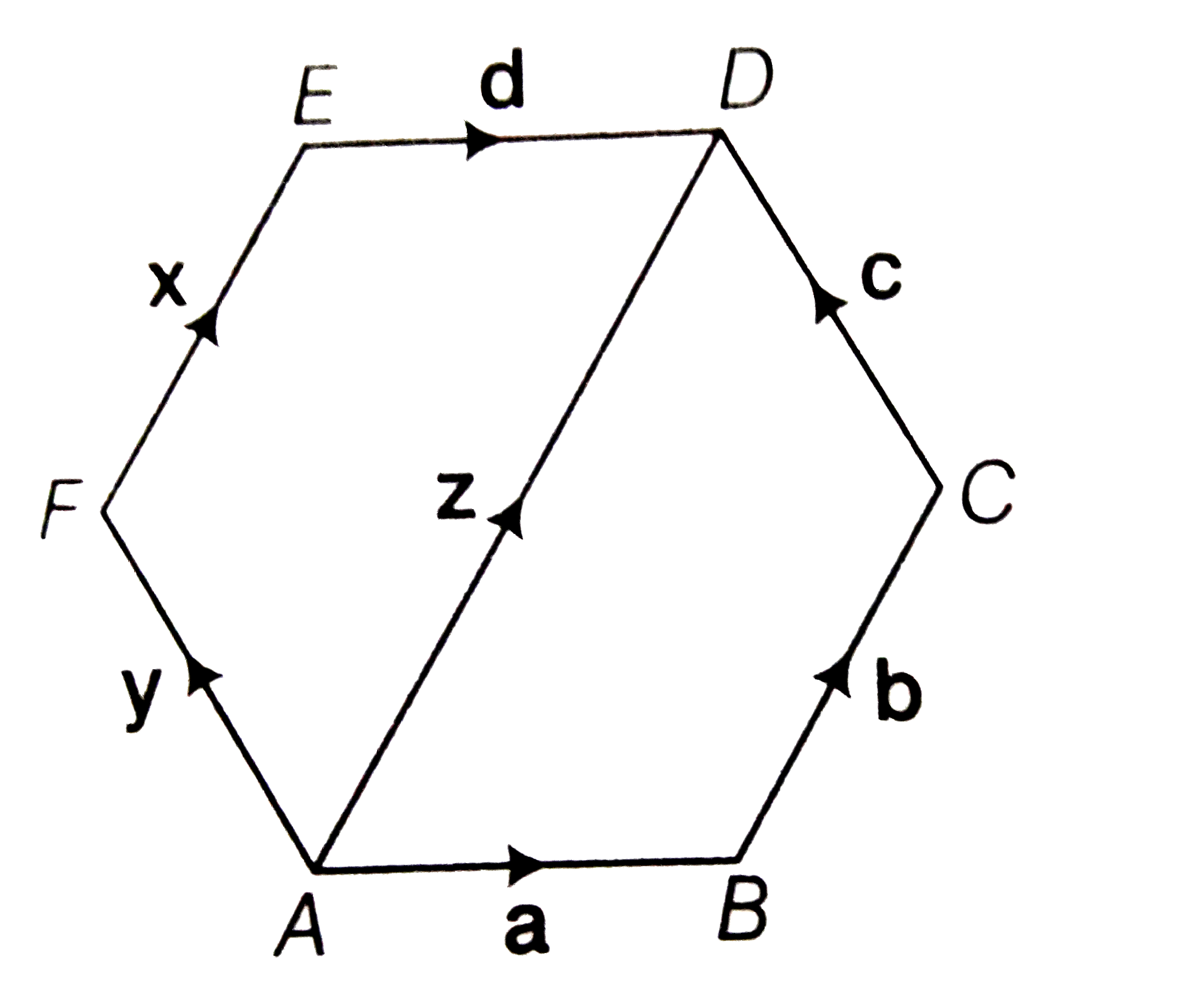
In Fig. ABCD is a regular hexagon, which vectors are: (i) Collinear (ii) Equal (iii) Coinitial (iv) Collinear but not equal
To solve the problem regarding the vectors in a regular hexagon ABCD, we will analyze the vectors step by step based on the definitions provided for collinear, equal, co-initial, and collinear but not equal vectors.
Step 1: Identify Collinear Vectors
Collinear vectors are those that lie along the same line or have the same direction.
- Vectors X and B: Both vectors point in the same direction.
- Vector Z: It also points in the same direction as X and B.
- Vectors Y and C: Both vectors point in the same direction.
- Vectors A and D: Both vectors point in the same direction.
Collinear Vectors:
- X, B, Z
- Y, C
- A, D
Step 2: Identify Equal Vectors
Equal vectors have the same magnitude and direction.
- Vectors A and D: They have the same length and direction.
- Vectors X and B: They also have the same length and direction.
- Vectors Y and C: They have the same length and direction.
Equal Vectors:
- A, D
- X, B
- Y, C
Step 3: Identify Co-initial Vectors
Co-initial vectors are those that start from the same point.
- Vectors A, Y, and Z: All start from point A.
Co-initial Vectors:
- A, Y, Z
Step 4: Identify Collinear but Not Equal Vectors
Collinear but not equal vectors are those that have the same direction but different magnitudes.
- Vectors X and Z: They point in the same direction but have different lengths.
- Vectors Z and B: They point in the same direction but have different lengths.
Collinear but Not Equal Vectors:
- X, Z
- Z, B
Final Summary of Vectors
1. Collinear Vectors: X, B, Z; Y, C; A, D
2. Equal Vectors: A, D; X, B; Y, C
3. Co-initial Vectors: A, Y, Z
4. Collinear but Not Equal Vectors: X, Z; Z, B
---
Collinear vectors are those that lie along the same line or have the same direction.
- Vector Z: It also points in the same direction as X and B.
- Vectors Y and C: Both vectors point in the same direction.
- Vectors A and D: Both vectors point in the same direction.
- X, B, Z
- Y, C
- A, D
Equal vectors have the same magnitude and direction.
- Vectors X and B: They also have the same length and direction.
- Vectors Y and C: They have the same length and direction.
- A, D
- X, B
- Y, C
Co-initial vectors are those that start from the same point.
- A, Y, Z
Collinear but not equal vectors are those that have the same direction but different magnitudes.
- Vectors Z and B: They point in the same direction but have different lengths.
- X, Z
- Z, B
1. Collinear Vectors: X, B, Z; Y, C; A, D
2. Equal Vectors: A, D; X, B; Y, C
3. Co-initial Vectors: A, Y, Z
4. Collinear but Not Equal Vectors: X, Z; Z, B
Topper's Solved these Questions
Similar Questions
In the given figure, ABCDEF is a regular hexagon, which vectors are:
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
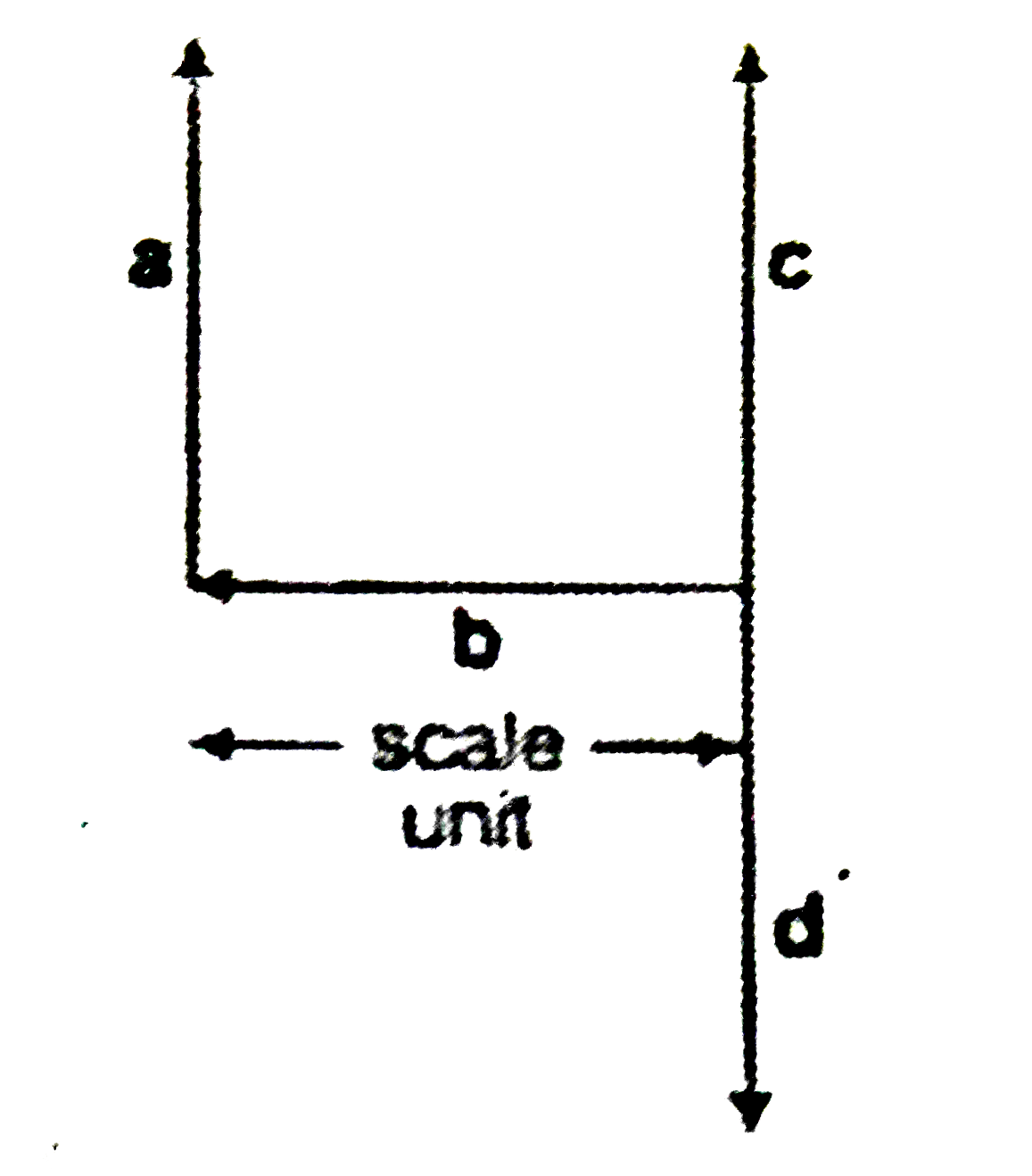
View SolutionIn the following figure, which of the vectors are:
(i) Collinear
(ii) Equal
(iii) Co-initial
(iv) collinear but not equal .
View SolutionIn fig 23.3, which of the vectors are: i.Collinear ii. Equal iii. Co-initial
View SolutionIn the given figure, which of the vectors are :
(a) Collinear
(b) Equal
(C ) Colinitial
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, collinear
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, Collinear but not equal
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, equal
View SolutionIn the given figure, vectors which are
Collinear
Equal
Collinear but not equal.

View SolutionIn a fig 23.4 (a square), identify the following vectors: i.Coinitial ii.Equal iii.Collinear but not equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear but not equal
View Solution
