A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in Figure. What is the total length of such a spiral made up of thirteen consecutive
semicircles? (Take π=227)

Circumference of the semicircle = 12×2πr=πr
Circumference of first semicircle = π×0.5
Circumference of second semicircle = π×1.0
Circumference of third semicircle = π×1.5
And so on Circumference of 13th semicircle = π×6.5
Hence, series with common difference of 0.5π
Hence, sum of the series is
S=n2(a+l)
S=132(0.5π+6.5π)
S=45.5π
Thus, length of spiral is = 45.5π
=227×45.5
=143
Length of spiral is 143cm.
Topper's Solved these Questions
Similar Questions
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take π=22/7 ) (FIGURE)
View SolutionA biconvex lens is made of glass with refractive index 1.5 and has radii of curvature 20 cm and 30 cm. If the 20 cm surface is silvered, what is the effective focal length of the mirror formed?

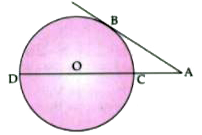
View SolutionIn the given figure O is the centre of the circle and AB is a tangents at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle.
View SolutionThe radii of the ends of a bucket of height 24 cm are 15 cm and 5 cm. Find its capacity. (Take π=22/7 )
View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View SolutionThe length of the plastic tube of the refill of a dot pen is (12.7±0.1) cm and the length of the metal nib is (1.40±0.2)cm. What is the total length of the refill?
View SolutionA rectangle is made up of 12 square of side 1 cm. What possible dimensions can the rectangle have ?
View SolutionA rectangle is made up of 16 squares of side 1 cm each. What possible dimensions can the rectangle have ?
View SolutionTwo objects A and B are of lengths 5 cm and 7cm determined with errors 0.1 cm and 0.2 cm respectively.What is the error in determing (a) the total length and (b) the difference in their lengths?
View Solution
