Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
By pythagoras theorem,
OA2=AP2+OP2
In △BPO
OB2=BP2+OP2
from above we get
AP=BP
Hence proved.
Topper's Solved these Questions
Similar Questions
In two concentric circle, prove that a chord of larger circle which is tangent to smaller circle is bisected at the point of contact.
View SolutionIn two concentric circles prove that all chords of the outer circle which touch the inner circle are of equal length.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm. and 3 c. Find the length of the chord of the larger circle which touches the cmaller circle.
View SolutionThe shows two concentric circles and AD is a chord of lenger circle. prove that AB=CD
View SolutionFind the area of the region between the two concentric circles, if the length of a chord of the outer circle just touching the inner circle at a particular point on it is 10 cm (Take, π=227)
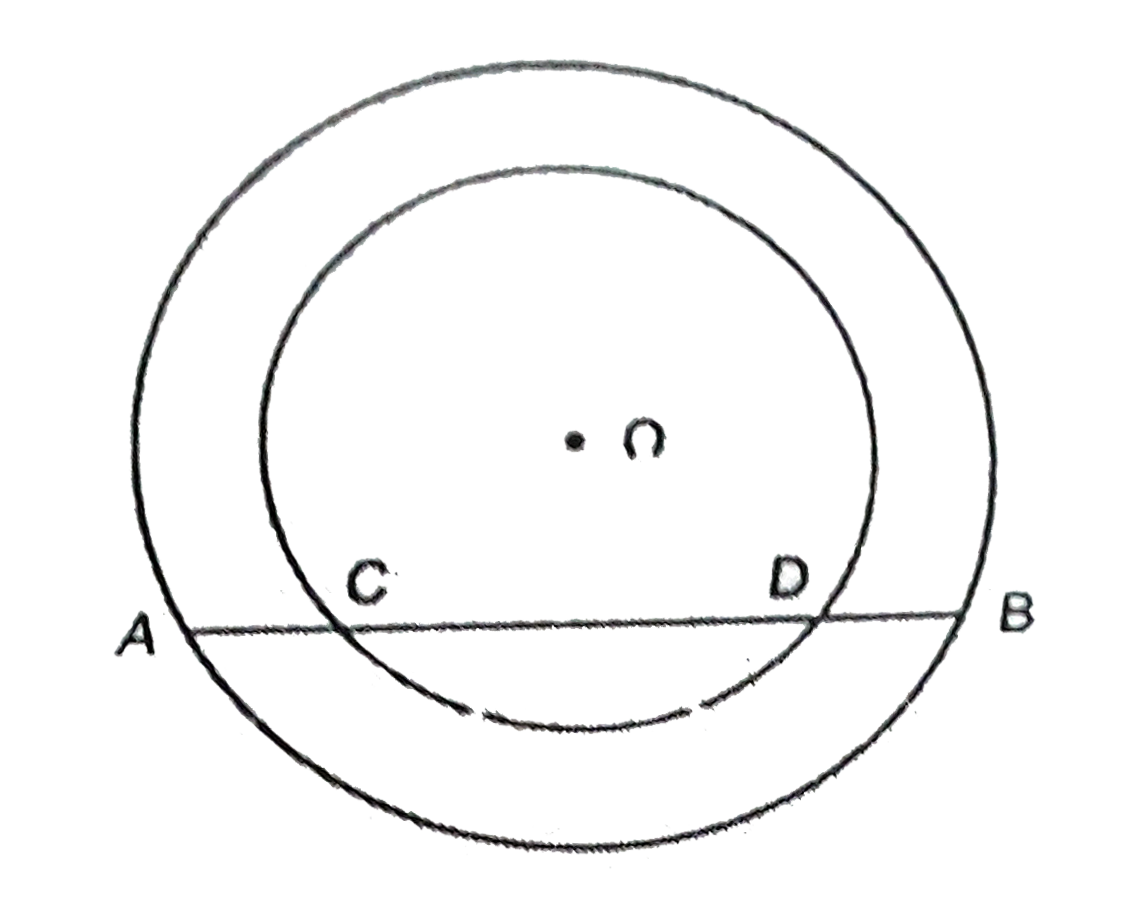
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
View SolutionThe locus of the centre of a circle which touches two given circles externally is a
View Solution
