BL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2
Please refer to diagram in video.
As BL and CM are median to AC and AB.
So, AM=BM=12AB
and CL=AL=12CA
Now, in ΔABL,
BL2=AL2+AB2
BL2=(AC2)2+AB2=AC24+AB2
⇒4BL2=AC2+4AB2→(1)
Similarly, in ΔACM,
CM2=AM2+AC2
CM2=(AB2)2+AC2=AB24+AC2
⇒4CM2=4AC2+AB2→(2)
Adding (1) and (2),
4BL2+4CM2=AC2+4AB2+4AC2+AB2
⇒4(BL2+CM2)=5(AB2+AC2)
⇒4(BL2+CM2)=5BC2
Similar Questions
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2+BD2=AB2+DE2 .
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2+BD2=AB2+DE2.
View SolutionABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
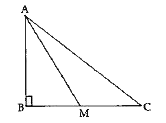
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
AM2+BC2=AC2+BM2
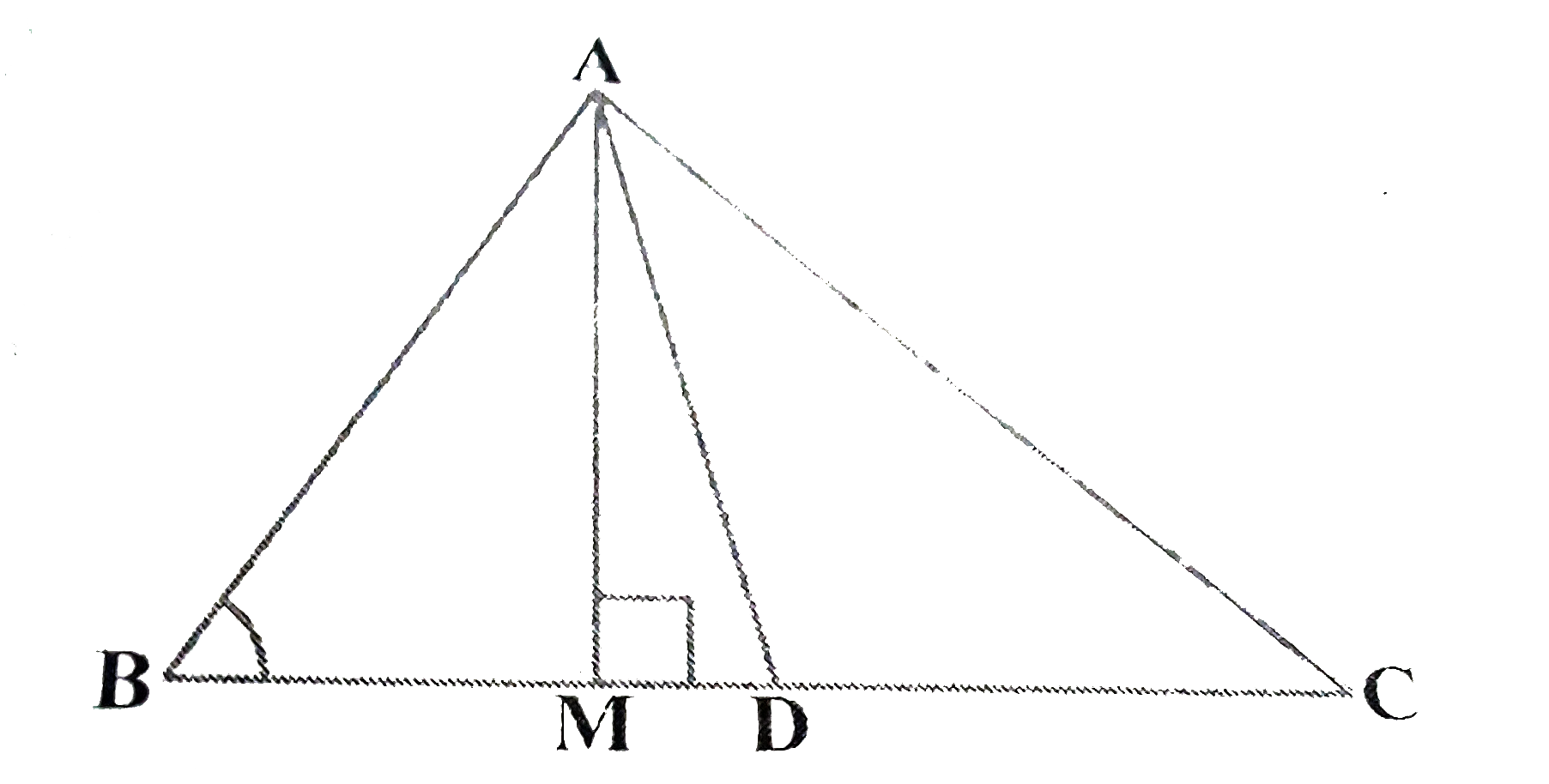
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View SolutionThe points A(3,0) , B (a, -2) and C(4, -1) are the vertices of triangle ABC right angled at vertex A. Find the value of a.
View SolutionIn triangle ABC is right-angled at B. Given that AB=9cm, AC=15cmcalculate B C.
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP

View Solution
