ABC is an isosceles right triangle, right-angled at $C$ . Prove that: $A B^{2} = 2 A C^{2} .$

Video Solution

Text Solution

Verified by Experts

In $Δ A B C, ∠ A C B = 90 °$ and $A C = B C$ [Since, ABC is an isosceles triangle right angled at C]
Using Pythagoras theorem,
$\Rightarrow {(A B)}^{2} = {(A C)}^{2} + {(B C)}^{2}$
$\Rightarrow {(A B)}^{2} = {(A C)}^{2} + {(A C)}^{2}$ [Since AC = BC]
Therefore, ${(A B)}^{2} = 2 {(A C)}^{2}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Similar Questions

$A B C$ is an isosceles right triangle right-angled at $C$ . Prove that $A B^{2} = 2 A C^{2}$ .
View Solution
ABC is a isosceles right angled triangle, right angled at C. prove that $A B^{2} = 2 A C^{2}$
View Solution
In figure ABC is an isosceles triangle , right angled at C . Therefore

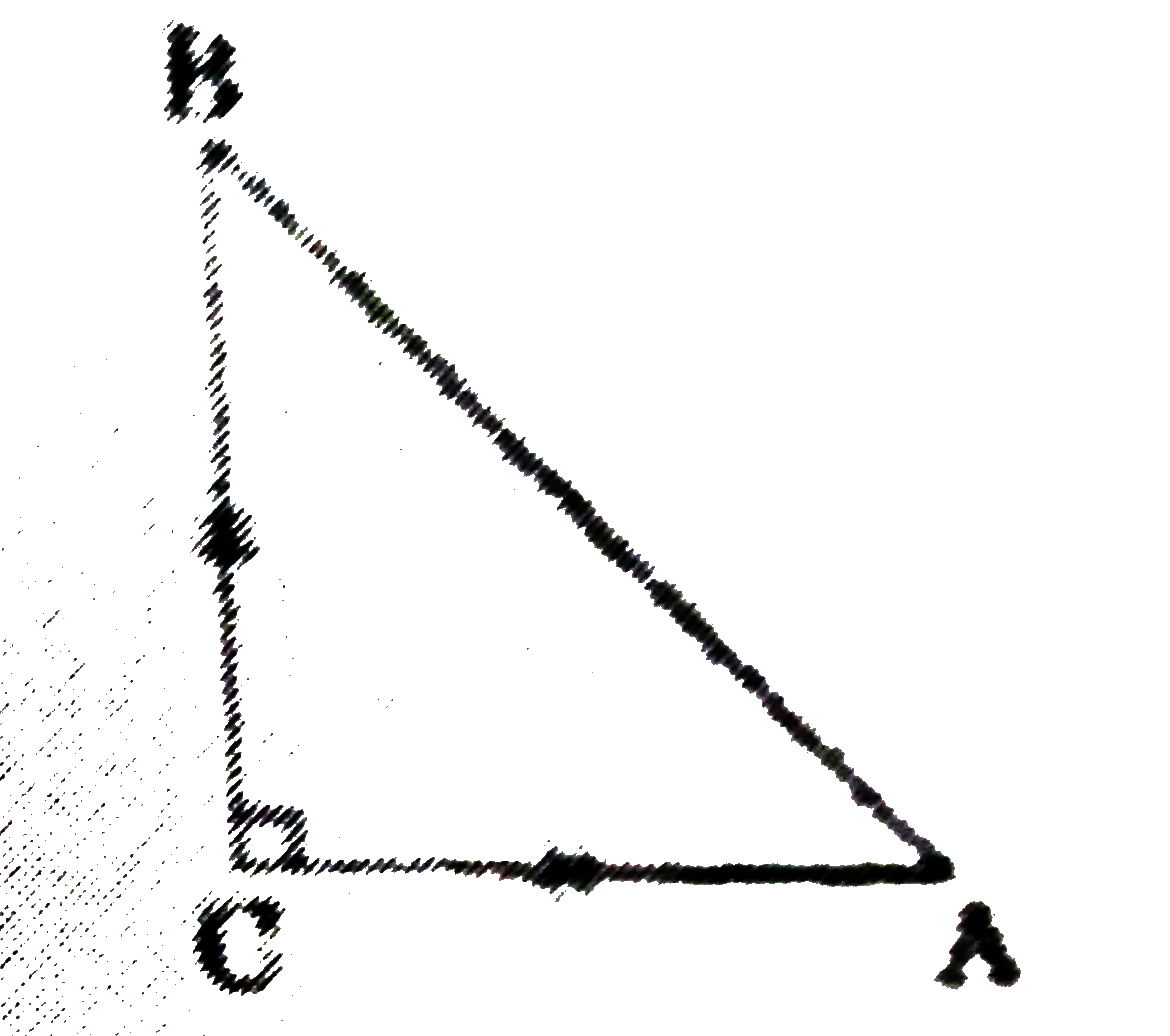
View Solution
$A B C$ is an isosceles right-triangle right angled at $C$ such that $A C = 5 c m .$ Then, $A B =$ (a) 2.5 cm (b) $5 \sqrt{2}$ cm (c) 10 cm (d) 5 cm
View Solution
$A B C$ is a right triangle right-angled at $C a n d A C = \sqrt{3} B C$ . Prove that $∠ A B C = 60^{0} .$
View Solution
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that $A E^{2} + B D^{2} = A B^{2} + D E^{2}$ .
View Solution
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that $A E^{2} + B D^{2} = A B^{2} + D E^{2}$ .
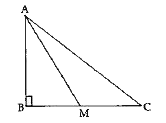
View Solution
ABC is a triangle, right angled at B, M is a point on BC. Prove that :
$A M^{2} + B C^{2} = A C^{2} + B M^{2}$

View Solution
BL and CM are medians of a triangle ABC right angled at A. Prove that $4 (B L^{2} + C M^{2}) = 5 B C^{2}$
View Solution
Let the complex numbers $Z_{1}, Z_{2} and Z_{3}$ are the vertices A, B and C respectively of an isosceles right - angled triangle ABC with right angle at C, then the value of $\frac{{(Z_{1} - Z_{2})}_{1}^{2}}{(Z_{1} - Z_{3}) (Z_{3} - Z_{2})}$ is equal to
View Solution

Recommended Questions

Home
Ask Doubt
Profile