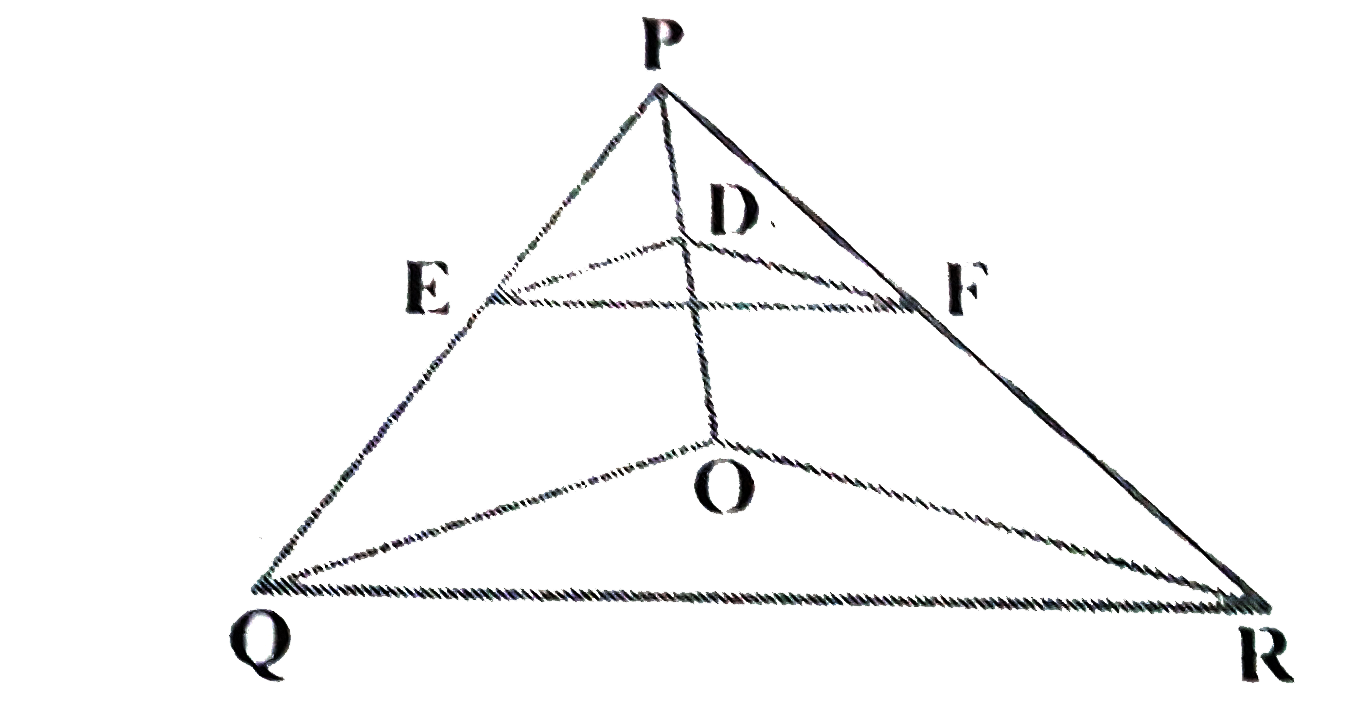
In figure DE || OQ and DF || OR. Show that EF||QR.
Video Solution
Text Solution
In △POQ, DE∣∣OQ, (given)
By basic proportionality theorem, we have,
PEEQ=PDDO ...(i)
Similarly,
In △POR, DF∣∣OR, (given)
By basic proportionality theorem, we have,
PDDO=PFFR ...(ii)
Now, from (i) and (ii),
PEEQ=PFFR
Which gives, EF∣∣QR
Hence proved.
|
Similar Questions
In the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

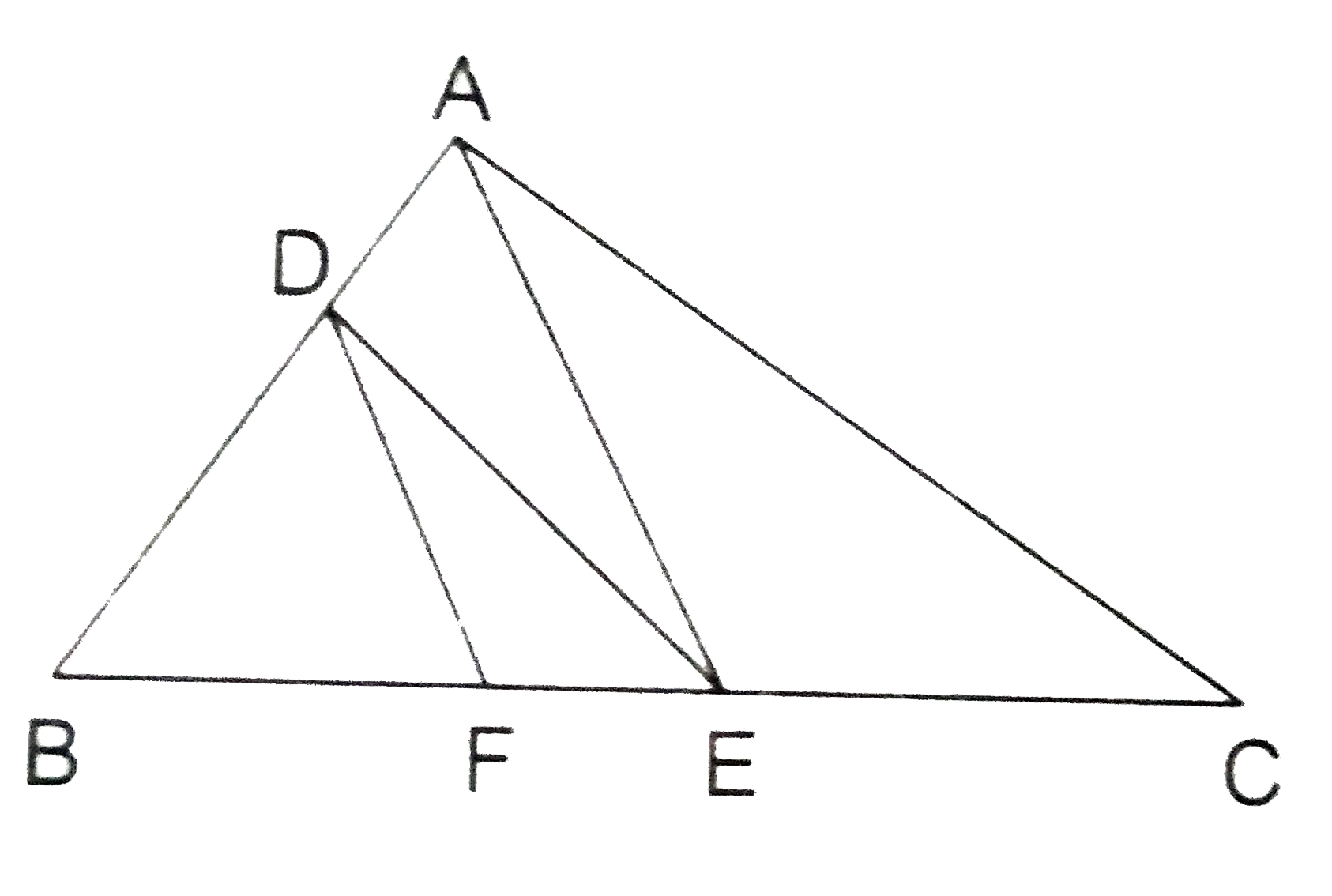
View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC
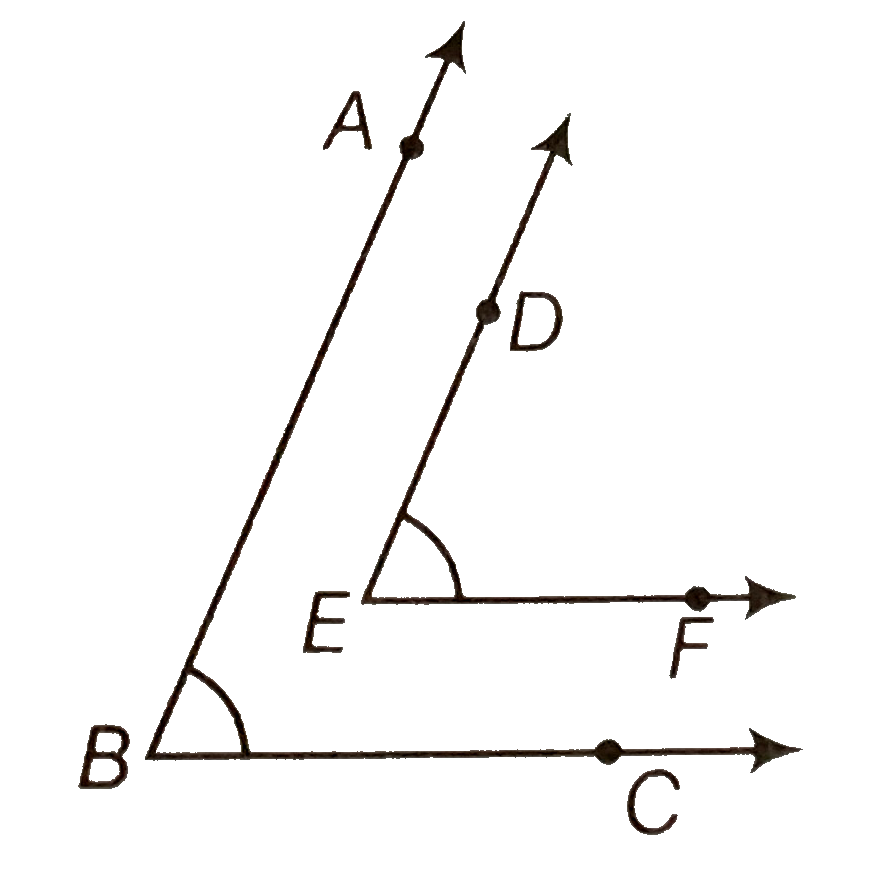
View SolutionIn the figure, BA|| ED and BC|| EF. Show that ∠ABC = ∠DEF.
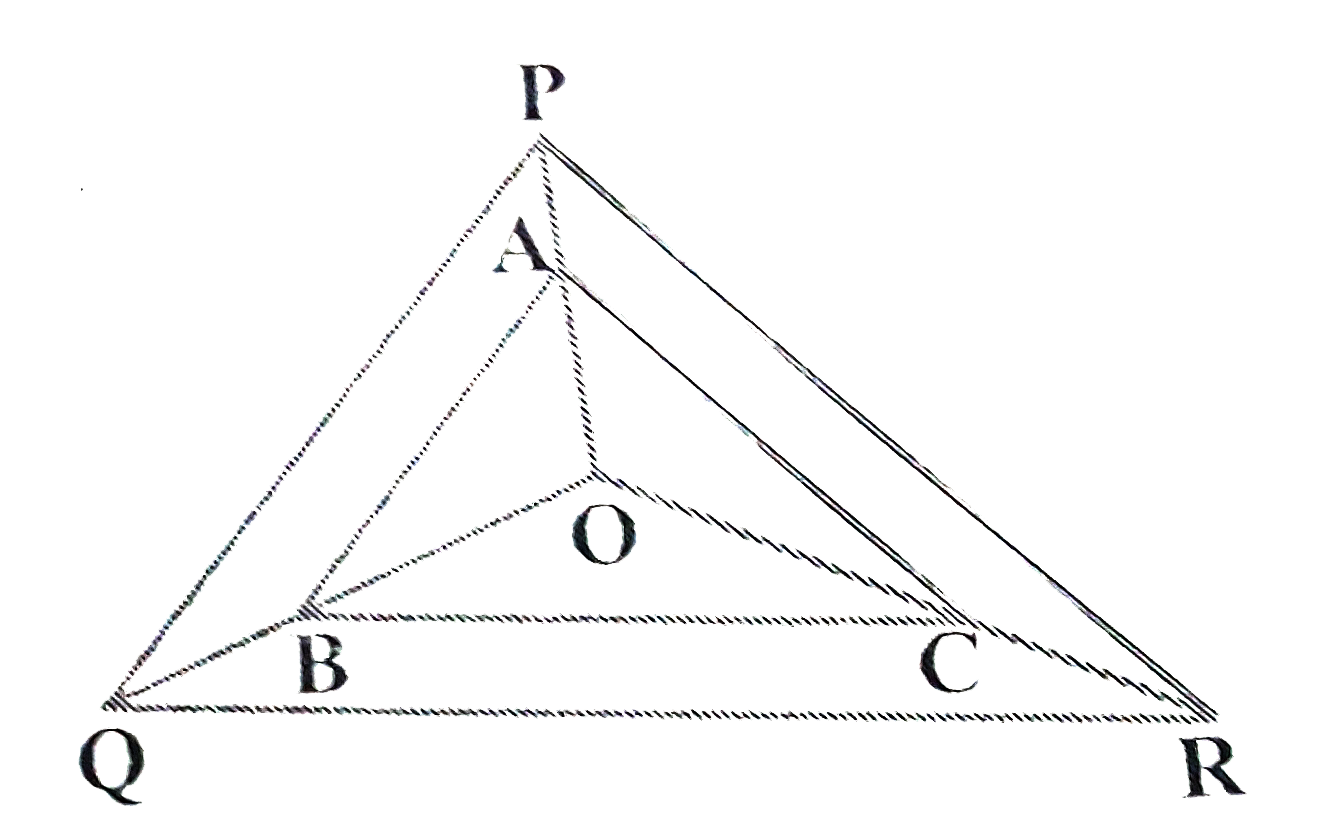
View SolutionIn figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

View SolutionIn Figure DE||BC and CD||EF. Prove that AD2=AB⋅AF.
View SolutionIn the figure, BA ∣∣ ED and BC ∣∣ EF. Show ∠ABC+∠DEF=180∘.
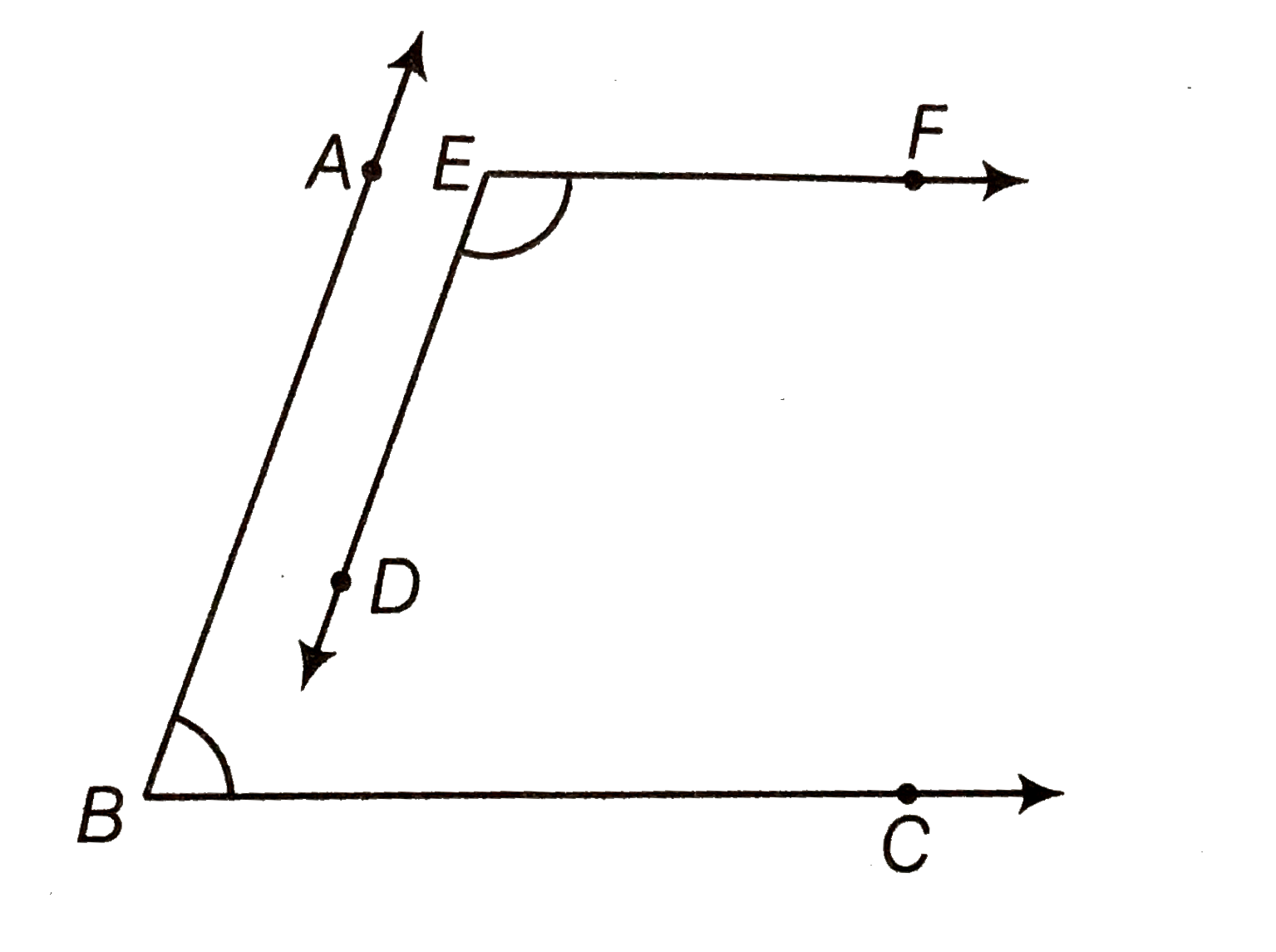
View SolutionIn the given figure A, B and C are points on OP, OQ and OR respectively such that AB||PQ and BC||QR. Show that AC||PR.

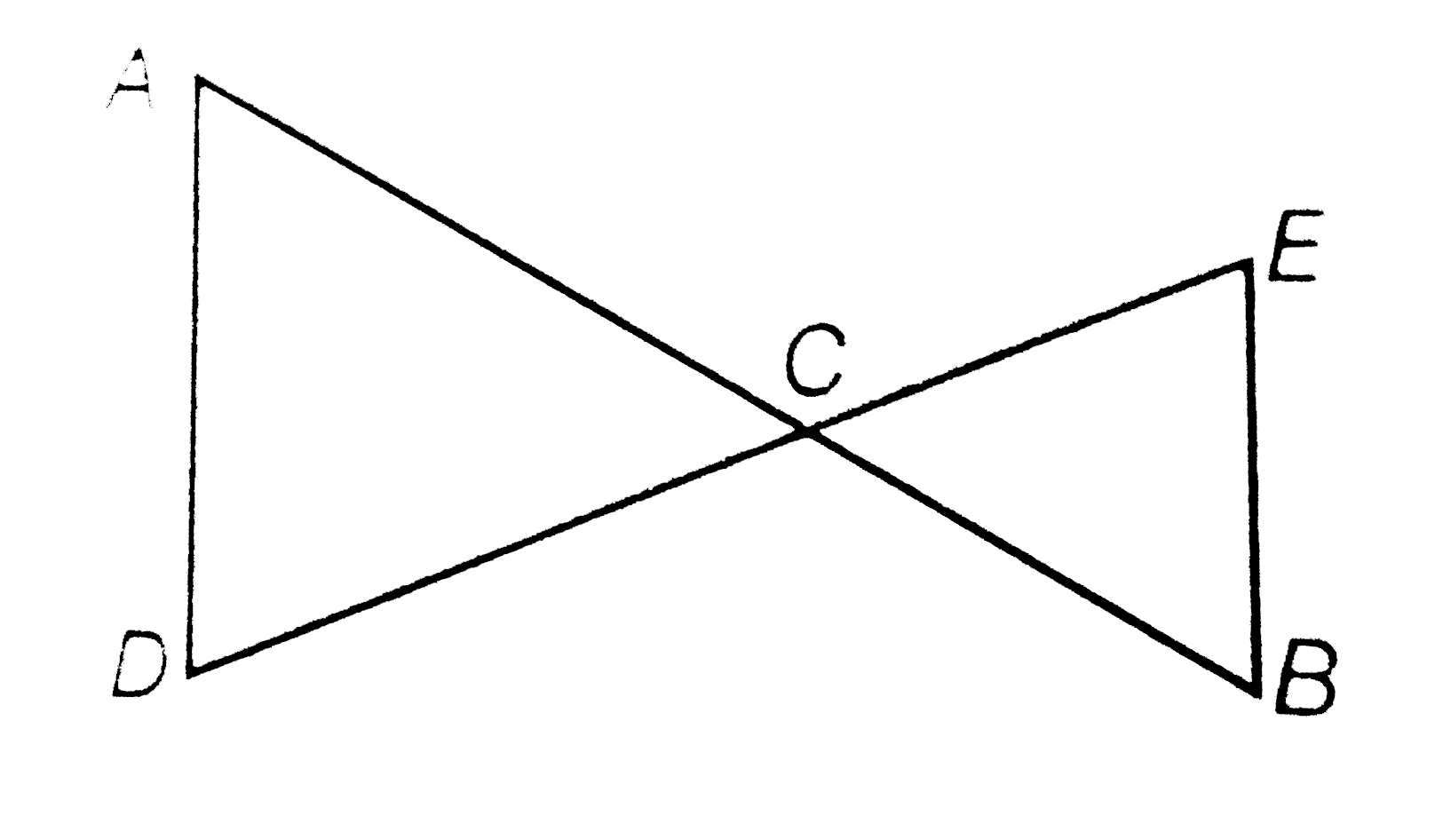
View SolutionIn the adjoining figure , we have AC=DC and CB = CE. Show that AB=DE.
View Solution
