In Figure DE||BC and CD||EF. Prove that AD2=AB⋅AF.
To prove that AD2=AB⋅AF, we will use the Basic Proportionality Theorem (also known as Thales' theorem).
1. Identify the Triangles and Parallel Lines:
Given that DE∥BC and CD∥EF, we can analyze the triangles formed by these parallel lines.
2. Apply the Basic Proportionality Theorem in Triangle ABC:
In triangle ABC, since DE∥BC, by the Basic Proportionality Theorem, we have:
ABAD=ACAE(1)
3. Apply the Basic Proportionality Theorem in Triangle ADC:
In triangle ADC, since CD∥EF, again by the Basic Proportionality Theorem, we have:
ADAF=ACAE(2)
4. Set the Ratios Equal:
From equations (1) and (2), we have:
ABAD=ACAE=ADAF
5. Cross-Multiply the Ratios:
From the equality ABAD=ADAF, we can cross-multiply:
AB⋅AF=AD⋅AD
This simplifies to:
AD2=AB⋅AF
6. Conclusion:
Hence, we have proved that:
AD2=AB⋅AF
Therefore, the statement is proved.
Given that DE∥BC and CD∥EF, we can analyze the triangles formed by these parallel lines.
In triangle ABC, since DE∥BC, by the Basic Proportionality Theorem, we have:
ABAD=ACAE(1)
In triangle ADC, since CD∥EF, again by the Basic Proportionality Theorem, we have:
ADAF=ACAE(2)
From equations (1) and (2), we have:
ABAD=ACAE=ADAF
From the equality ABAD=ADAF, we can cross-multiply:
AB⋅AF=AD⋅AD
This simplifies to:
AD2=AB⋅AF
Hence, we have proved that:
AD2=AB⋅AF
Therefore, the statement is proved.
Topper's Solved these Questions
Similar Questions
In the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

View SolutionIn Figure, DE∣∣AC and DF∣∣AE . Prove that EFBF=ECBE .
View SolutionIn the given figure DE||AC and DC||AP. Prove that BEEC=BCCP

View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionIn Figure 3, AD⊥BC and BD=13CD. Prove that 2CA2=2AB2+BC2.
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

View SolutionIn the following figure, DE||AC and DC||AP. Prove that : BEEC=BCCP
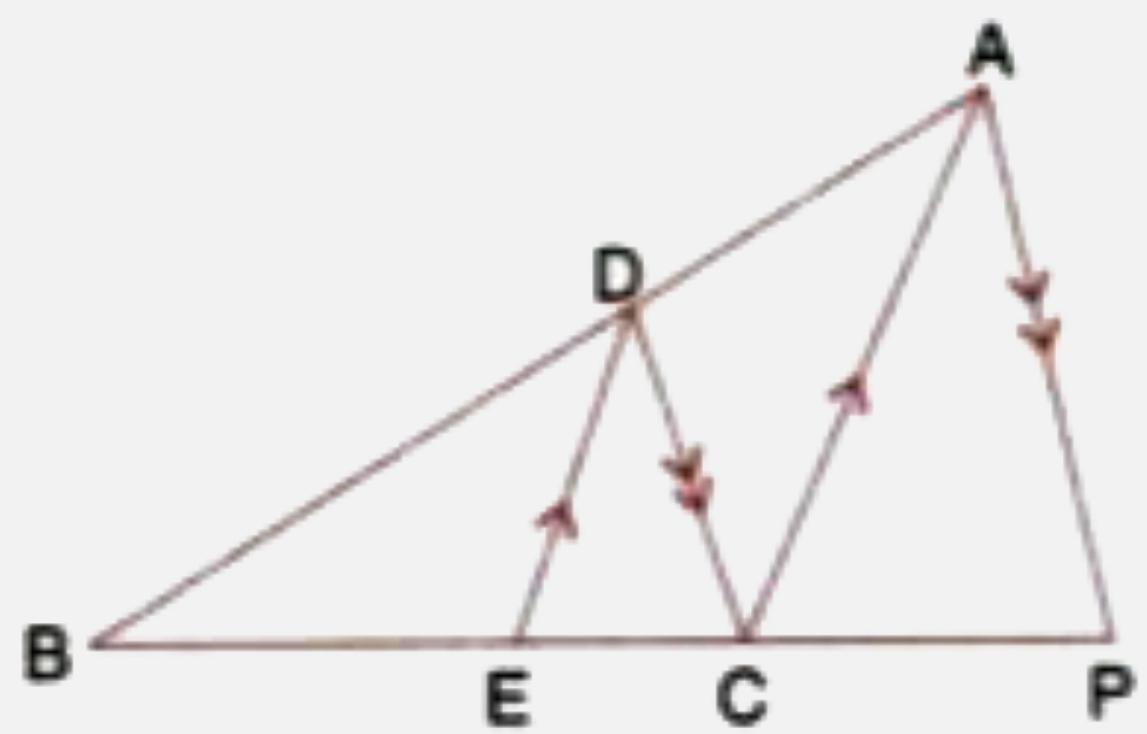
View SolutionIn figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=EF.
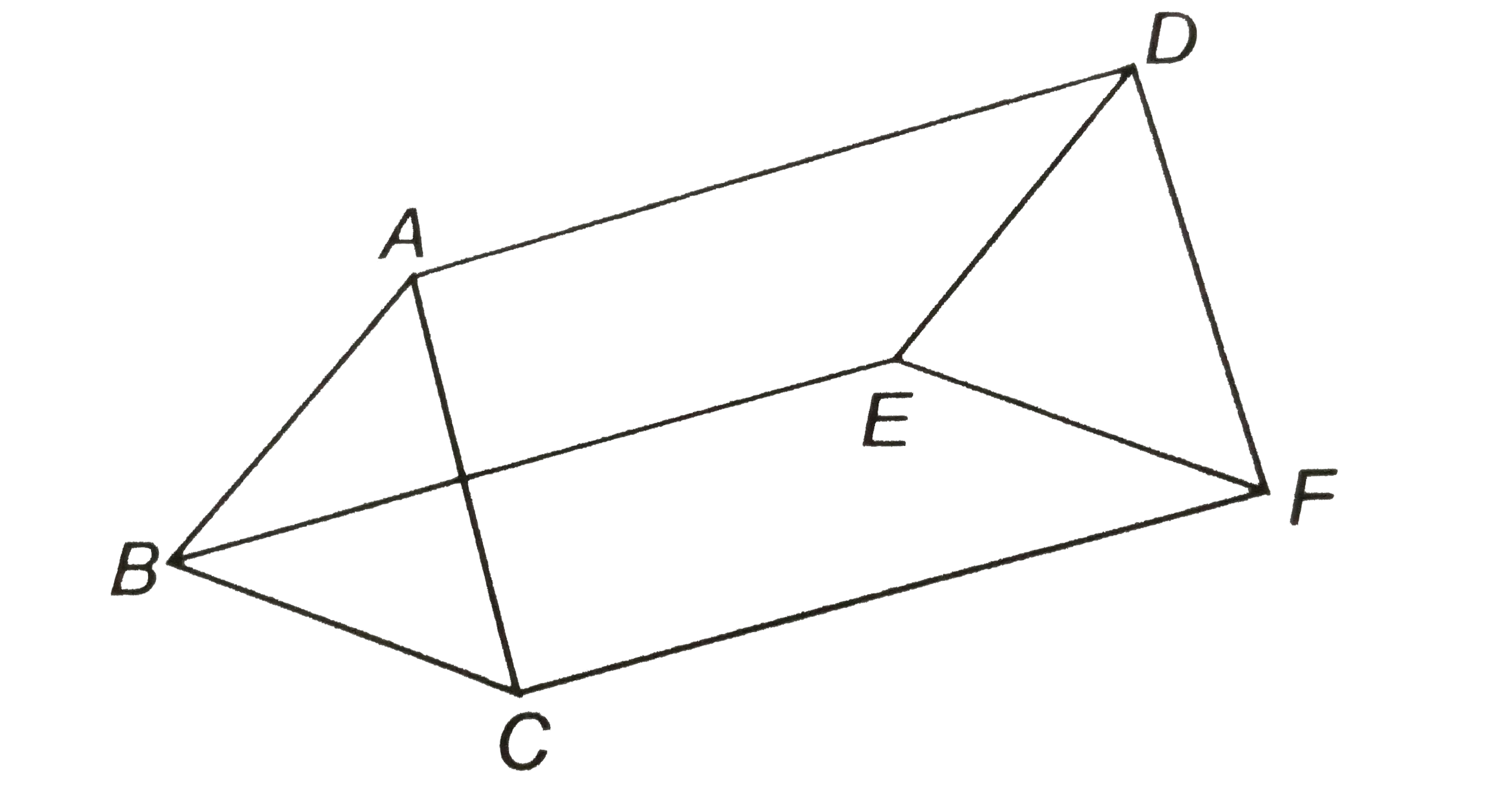
View SolutionIn the given figure D is mid-point of AB. DE//BC and DF //AC . Prove that : DE = BF

View SolutionIn Figure , If PQ || BC and PR || CD, prove that QBAQ=DRAR .
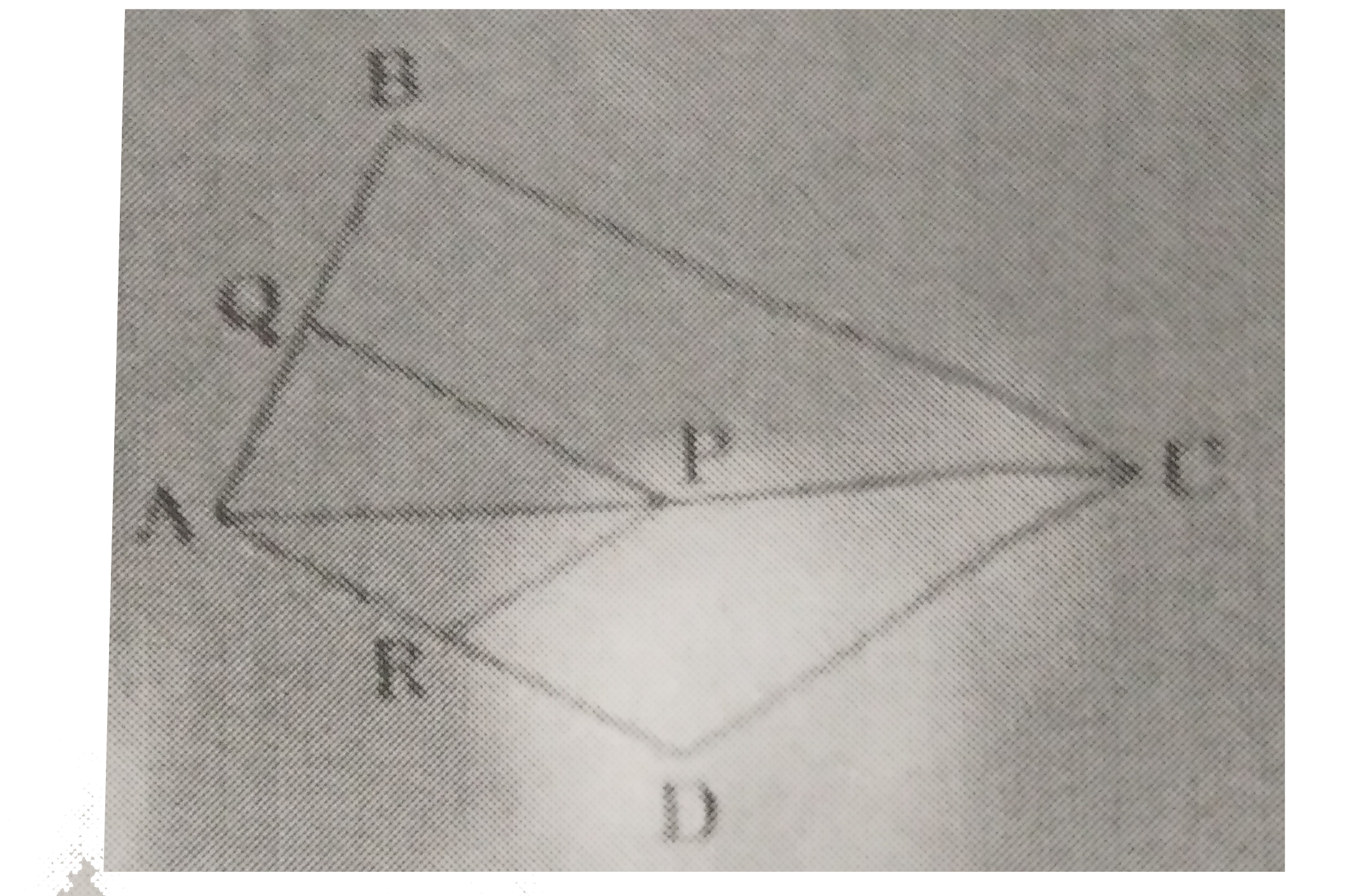
View Solution
