Fig. 12.3 depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
To find the area of each of the five scoring regions of the archery target, we will follow these steps:
Step 1: Calculate the radius of the Gold region.
- The diameter of the Gold region is given as 21 cm.
- Radius (r) = Diameter / 2 = 21 cm / 2 = 10.5 cm.
Step 2: Calculate the area of the Gold region.
- Area of a circle = πr².
- Using π = 22/7, Area of Gold = (22/7) * (10.5)².
- Area of Gold = (22/7) * 110.25 = 346.5 cm².
Step 3: Calculate the radius of the Red region.
- The width of each band is 10.5 cm.
- Radius of Red = Radius of Gold + Width of Red = 10.5 cm + 10.5 cm = 21 cm.
Step 4: Calculate the area of the Red region.
- Area of Red + Gold = π * (21)² = (22/7) * 441 = 1386 cm².
- Area of Red = Area of Red + Gold - Area of Gold = 1386 cm² - 346.5 cm² = 1039.5 cm².
Step 5: Calculate the radius of the Blue region.
- Radius of Blue = Radius of Red + Width of Blue = 21 cm + 10.5 cm = 31.5 cm.
Step 6: Calculate the area of the Blue region.
- Area of Red + Blue = π * (31.5)² = (22/7) * 992.25 = 3118.5 cm².
- Area of Blue = Area of Red + Blue - Area of Red = 3118.5 cm² - 1386 cm² = 1732.5 cm².
Step 7: Calculate the radius of the Black region.
- Radius of Black = Radius of Blue + Width of Black = 31.5 cm + 10.5 cm = 42 cm.
Step 8: Calculate the area of the Black region.
- Area of Red + Blue + Black = π * (42)² = (22/7) * 1764 = 5544 cm².
- Area of Black = Area of Red + Blue + Black - Area of Red + Blue = 5544 cm² - 3118.5 cm² = 2425.5 cm².
Step 9: Calculate the radius of the White region.
- Radius of White = Radius of Black + Width of White = 42 cm + 10.5 cm = 52.5 cm.
Step 10: Calculate the area of the White region.
- Area of Gold + Red + Blue + Black + White = π * (52.5)² = (22/7) * 2756.25 = 8662.5 cm².
- Area of White = Area of Gold + Red + Blue + Black + White - Area of Gold + Red + Blue + Black = 8662.5 cm² - 5544 cm² = 3118.5 cm².
Summary of Areas:
- Area of Gold = 346.5 cm²
- Area of Red = 1039.5 cm²
- Area of Blue = 1732.5 cm²
- Area of Black = 2425.5 cm²
- Area of White = 3118.5 cm²
---
- The diameter of the Gold region is given as 21 cm.
- Radius (r) = Diameter / 2 = 21 cm / 2 = 10.5 cm.
- Area of a circle = πr².
- Using π = 22/7, Area of Gold = (22/7) * (10.5)².
- Area of Gold = (22/7) * 110.25 = 346.5 cm².
- The width of each band is 10.5 cm.
- Radius of Red = Radius of Gold + Width of Red = 10.5 cm + 10.5 cm = 21 cm.
- Area of Red + Gold = π * (21)² = (22/7) * 441 = 1386 cm².
- Area of Red = Area of Red + Gold - Area of Gold = 1386 cm² - 346.5 cm² = 1039.5 cm².
- Radius of Blue = Radius of Red + Width of Blue = 21 cm + 10.5 cm = 31.5 cm.
- Area of Red + Blue = π * (31.5)² = (22/7) * 992.25 = 3118.5 cm².
- Area of Blue = Area of Red + Blue - Area of Red = 3118.5 cm² - 1386 cm² = 1732.5 cm².
- Radius of Black = Radius of Blue + Width of Black = 31.5 cm + 10.5 cm = 42 cm.
- Area of Red + Blue + Black = π * (42)² = (22/7) * 1764 = 5544 cm².
- Area of Black = Area of Red + Blue + Black - Area of Red + Blue = 5544 cm² - 3118.5 cm² = 2425.5 cm².
- Radius of White = Radius of Black + Width of White = 42 cm + 10.5 cm = 52.5 cm.
- Area of Gold + Red + Blue + Black + White = π * (52.5)² = (22/7) * 2756.25 = 8662.5 cm².
- Area of White = Area of Gold + Red + Blue + Black + White - Area of Gold + Red + Blue + Black = 8662.5 cm² - 5544 cm² = 3118.5 cm².
- Area of Gold = 346.5 cm²
- Area of Red = 1039.5 cm²
- Area of Blue = 1732.5 cm²
- Area of Black = 2425.5 cm²
- Area of White = 3118.5 cm²
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES
6 Videos
- AREAS RELATED TO CIRCLESBOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Exercise 12.2
14 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - All Questions
65 Videos
Similar Questions
Figure, depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue Black and white. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
View SolutionTwo circles touch each other externally. The sum of their areas is 74πcm2 and the distance between their centres is 12 cm. Find the diameters of the circle.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. . If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionAB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig. 12.32). If ∠AOB=30∘, find the area of the shaded region.
View SolutionIf Figure - 4, AB and CD are two diameter of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. IF OA = 7 cm, then find the area of the shaded region.

View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
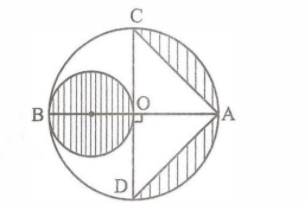
View SolutionIn the given figure, AB and CD are two diameters of circles ( with centre O) Perpendicular to each other and OD is the diameter of the smallest circle. If OA = 7cm, Find the area of the shaded region.
View SolutionThree circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region).
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View SolutionA wooden article was made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
View Solution
