In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
To locate a point in the interior of a triangle that is equidistant from all the sides, we can follow these steps:
1. Draw the Triangle: Begin by sketching a triangle ABC. Ensure that the triangle is not a right triangle, as the method will work for any type of triangle.
2. Draw the Angle Bisector of Angle B:
- Place the compass pointer at vertex B.
- Draw an arc that intersects both sides of the triangle (line AB and line BC).
- Label the points where the arc intersects line AB as D and line BC as E.
- Without changing the compass width, place the pointer at point D and draw another arc.
- Then, place the pointer at point E and draw another arc, ensuring that these two arcs intersect at point F.
- Draw a line from B through point F. This line is the angle bisector of angle B.
3. Draw the Angle Bisector of Angle C:
- Repeat the same process for angle C.
- Place the compass pointer at vertex C and draw an arc that intersects both sides of the triangle (line AC and line BC).
- Label the intersection points as G (on line AC) and H (on line BC).
- Using the same compass width, draw arcs from points G and H to find the intersection point I.
- Draw a line from C through point I. This line is the angle bisector of angle C.
4. Locate the Incenter:
- The point where the two angle bisectors (from steps 2 and 3) intersect is the incenter of the triangle. Label this point as O.
- This point O is equidistant from all three sides of the triangle.
5. Verification:
- To verify that point O is equidistant from all sides, you can measure the perpendicular distance from point O to each side of the triangle. All distances should be equal.
Conclusion:
The point O is the required point that is equidistant from all the sides of triangle ABC. This point is known as the incenter of the triangle.
---
- Place the compass pointer at vertex B.
- Draw an arc that intersects both sides of the triangle (line AB and line BC).
- Label the points where the arc intersects line AB as D and line BC as E.
- Without changing the compass width, place the pointer at point D and draw another arc.
- Then, place the pointer at point E and draw another arc, ensuring that these two arcs intersect at point F.
- Draw a line from B through point F. This line is the angle bisector of angle B.
- Repeat the same process for angle C.
- Place the compass pointer at vertex C and draw an arc that intersects both sides of the triangle (line AC and line BC).
- Label the intersection points as G (on line AC) and H (on line BC).
- Using the same compass width, draw arcs from points G and H to find the intersection point I.
- Draw a line from C through point I. This line is the angle bisector of angle C.
- The point where the two angle bisectors (from steps 2 and 3) intersect is the incenter of the triangle. Label this point as O.
- This point O is equidistant from all three sides of the triangle.
- To verify that point O is equidistant from all sides, you can measure the perpendicular distance from point O to each side of the triangle. All distances should be equal.
The point O is the required point that is equidistant from all the sides of triangle ABC. This point is known as the incenter of the triangle.
Topper's Solved these Questions
Similar Questions
ABC is a triangle. Locate a point in the interior of ΔABCwhich is equidistant from all the vertices of ΔABC
View SolutionIn triangle LMN, bisector of interior angles at L and N intersect each other at point A. Prove that :
point A is equidistant from all the three sides of the triangle.
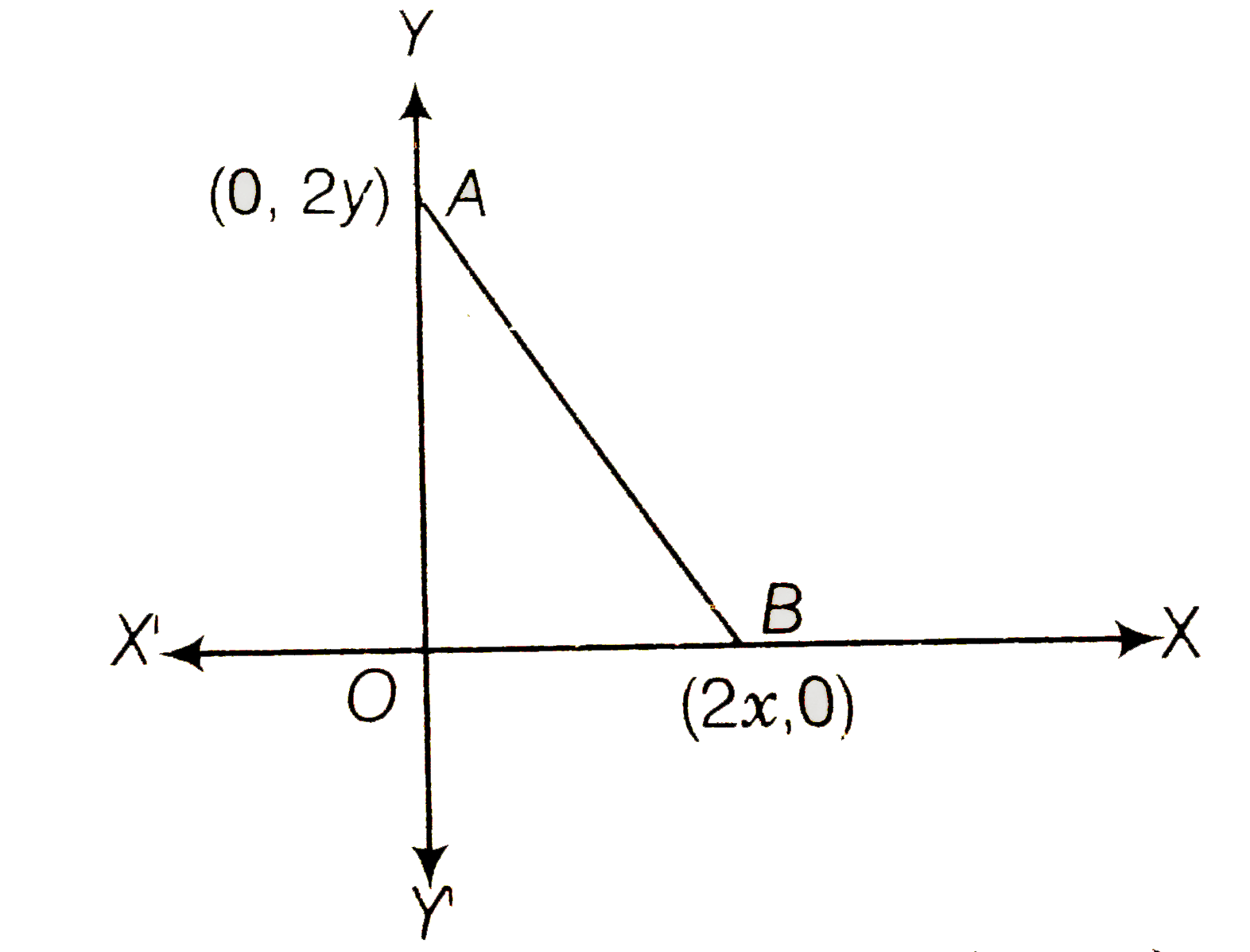
View SolutionThe coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
View SolutionA circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right-angled triangle whose radius of the circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. Area of Δ ABC is
View SolutionA circumcircle is a circle which passes through all vertices of a triangle and an incircle is a circle which is inscribed in a triangle touching all sides of a triangle. Let ABC be a right angled triangle whose radius of circumcircle is 5 and its one side AB = 6. The radius of incircle of triangle ABC is r. The value of r is
View SolutionThe mid-points of the sides of a triangle are (2,1),(−5,7)and(−5,−5). Find the equations of the sides of the triangle.
View SolutionLet the point P lies in the interior of an equilateral triangle with side lengths 2 units, each. Find the sum of the shortest distances from P to the sides of the triangle.
View SolutionSides of a triangle are in the ratio 3:4:5 and its area is 54cm2 Find the sides of the triangle.
View SolutionA point on the hypotenuse of a right triangle is at distances a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is (a23+b23)32
View SolutionFind a point on the base of a scalene triangle equidistant from its sides.
View Solution
