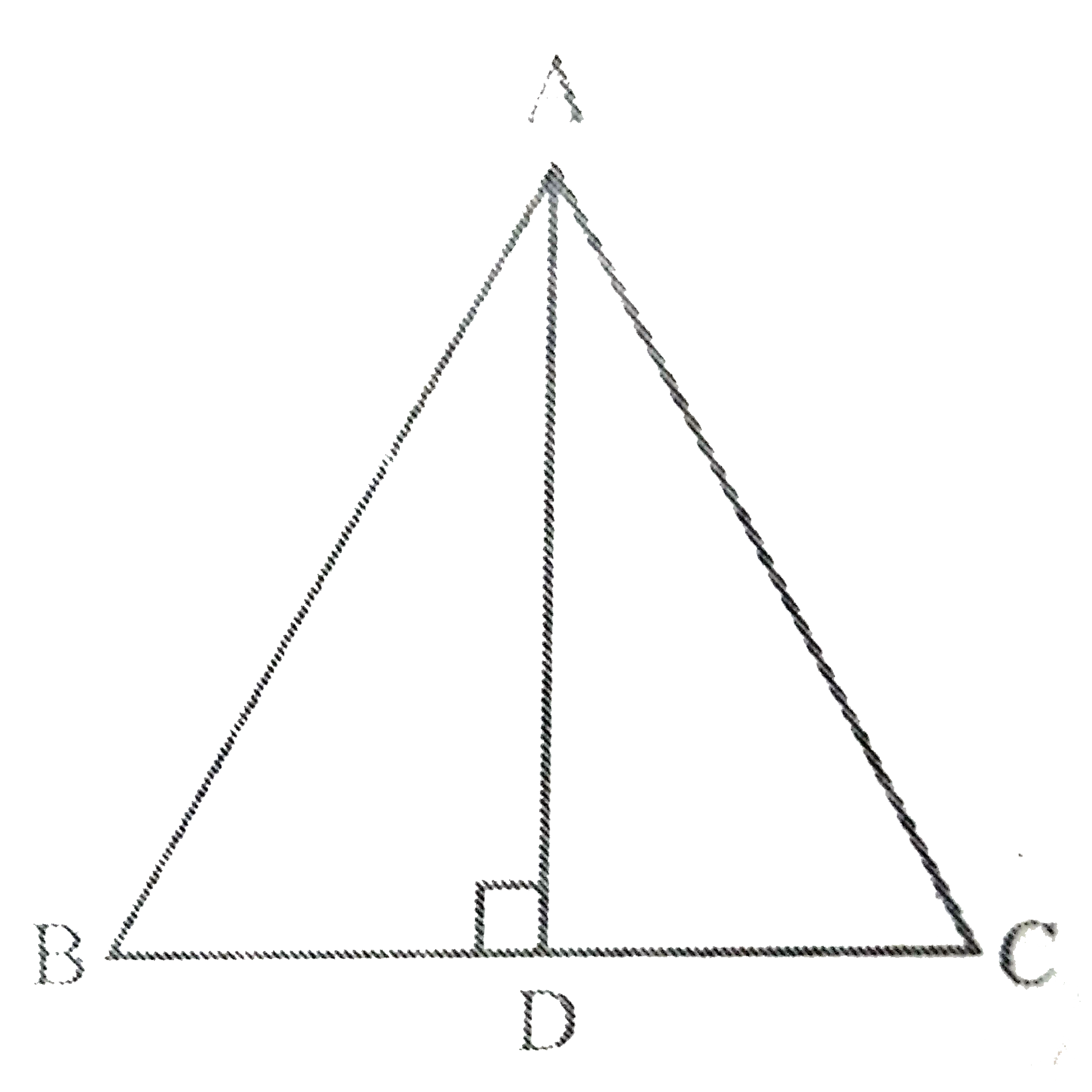
In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
(##IX07_E0202_s01##)
Given: AD is the perpendicular bisector of BC means ∠ADB=∠ADC=90∘ and BD=DC
To Prove: ΔABC is an isosceles triangle in which AB=AC.
In ΔADC and ΔADB,
AD=AD (Common)
∠ADC=∠ADB (Each 90∘)
CD=BD (AD is the perpendicular bisector of BC)
∴ΔADC≅ΔADB (By SAS congruence rule)
∴AB=AC (By CPCT)
Therefore, ABC is an isosceles triangle in which AB=AC.
Topper's Solved these Questions
Similar Questions
In Δ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
View SolutionIn triangle ABC,AD is perpendicular to side BC and AD2=BD×DC.
Show that angle BAC=90∘.
View SolutionIn a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
View SolutionIn any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD

View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
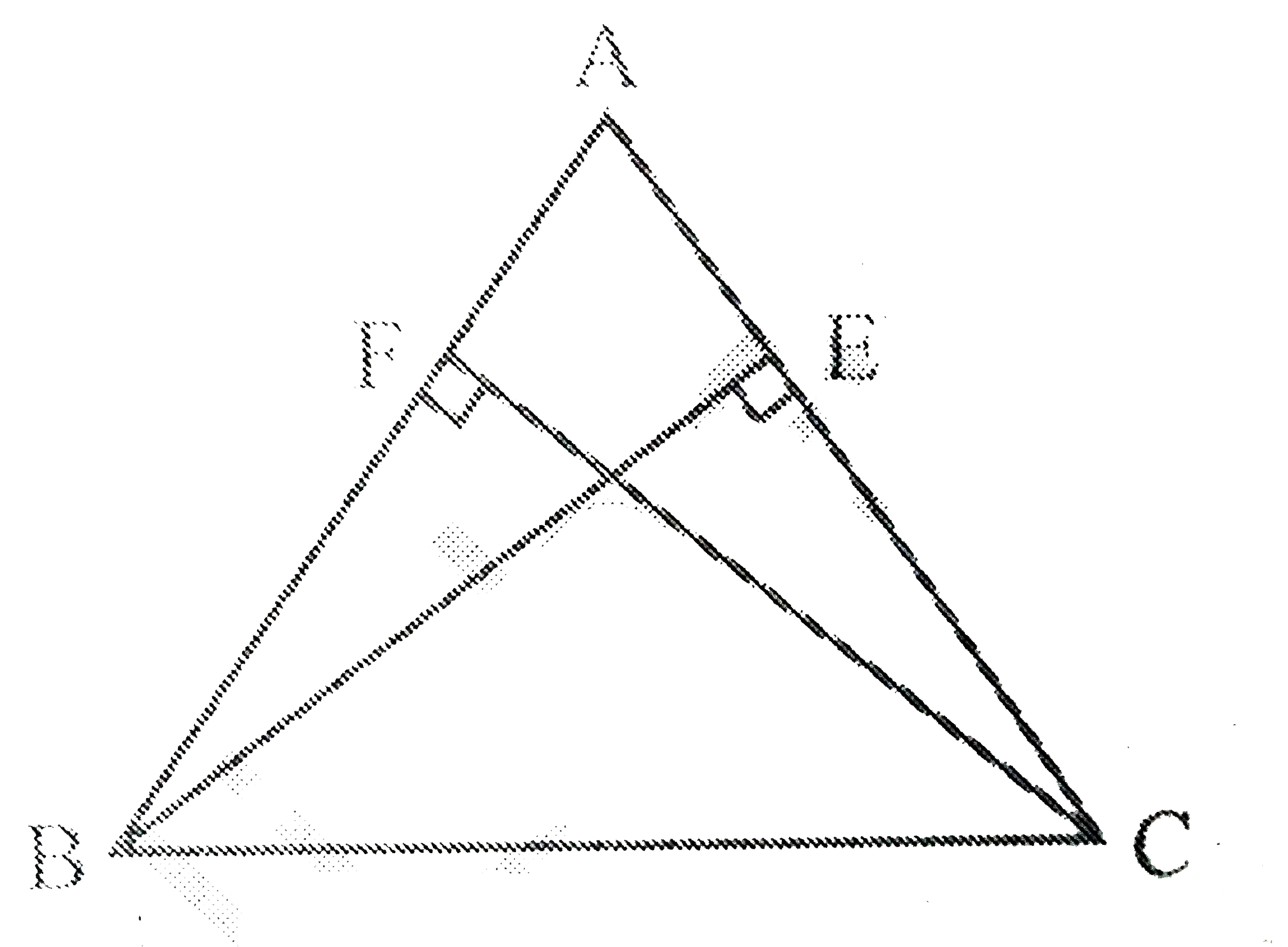
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

View SolutionIf median of the ΔABC through A is perpendicular to BC, then which one of the following is correct ?
View SolutionIn any triangle ABC, if the angle bisector of ∠Aand perpendicular bisector of BCintersect, prove that they intersect on the circumcircle of the triangle ABC
View SolutionABC is an isosceles triangle with AB= AC. Draw AP⊥BC to show that ∠B=∠C.
View Solution