Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
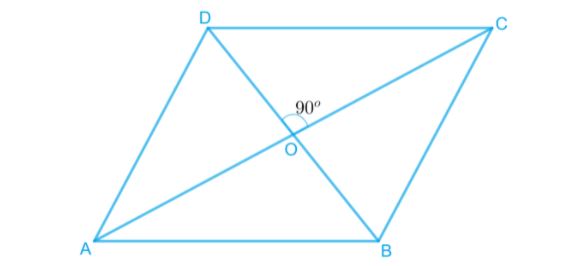
Given: The diagonals of a quadrilateral bisect each other at right angles.
To show that a given quadrilateral is a rhombus, we have to show it is a parallelogram and all the sides are equal.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus
Let ABCD be a quadrilateral, whose diagonals AC and BD bisect each other at the right angle.
So, we have, OA=OC,OB=OD, and ∠AOB=∠BOC=∠COD=∠AOD=90∘.
To prove ABCD a rhombus, we have to prove ABCD is a parallelogram and all the sides of ABCD are equal.
In ΔAOD and ΔCOD,
OA=OC (Diagonals bisect each other)
∠AOD=∠COD=90∘ (Given)
OD=OD (Common)
∴ΔAOD≅ΔCOD (By SAS congruence rule)
∴AD=CD (By CPCT) ...............(1)
Similarly, it can be proved that
AD=AB and CD=BC .................(2)
From Equations (1) and (2), AB=BC=CD=AD
Since opposite sides of quadrilateral ABCD are equal, it can be said that ABCD is a parallelogram. Since all sides of a parallelogram ABCD are equal, it can be said that ABCD is a rhombus.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES
8 Videos
- QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8.2
7 Videos
- PROBABILITYBOOK - NCERT ENGLISHCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES
10 Videos
- STATISTICSBOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - Exercise 14.2
9 Videos
Similar Questions
Prove that; If the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angle, then it is a square.
View SolutionShow that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionState True or False
If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.
View SolutionThe diagonals of a parallelogram bisect each other.
View SolutionProve that the diagonals of a parallelogram bisect each other.
View SolutionThe diagonals of a rectangle bisect each other
View Solution
