Show that the diagonals of a square are equal and bisect each other at right angles.

Video Solution

Text Solution

Verified by Experts

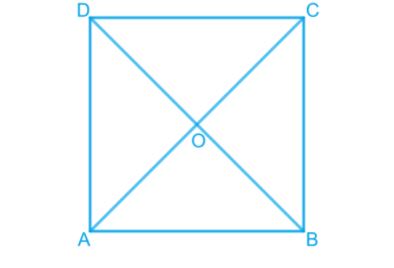
Given: The quadrilateral is a square.
To prove: Diagonals of a square are equal and bisect each other at right angles.
Thus, we have to prove $A C = B D, O A = O C, O B = O D$ , and $∠ A O B = 90^{\circ}$
Let $A B C D$ be a square.
Let the diagonals $A C$ and $B D$ intersect each other at a point $O$ .
In $Δ A B C$ and $Δ D C B$ ,
$A B = D C$ (Sides of a square are equal to each other)
$∠ A B C = ∠ D C B$ (All interior angles are of 90^@)
$B C = C B$ (Common side)
$∴ Δ A B C ≅ Δ D C B$ (By SAS congruence rule)
$∴ A C = D B$ (By CPCT) ------------ (1)
Hence, the diagonals of a square are equal in length.
In $Δ A O B$ and $Δ C O D$ ,
$∠ A O B = ∠ C O D$ (Vertically opposite angles)
$∠ A B O = ∠ C D O$ (Alternate interior angles)
$A B = C D$ (Sides of a square are always equal)
$∴ Δ A O B ≅ Δ C O D$ (By AAS congruence rule)
$∴ A O = C O$ and $O B = O D$ (By CPCT) ------------ (2)
Hence, the diagonals of a square bisect each other.
In $Δ A O B$ and $Δ C O B$ ,
As we had proved that diagonals bisect each other,
Therefore, $A O = C O$
$A B = C B$ (Sides of a square are equal)
$B O = B O$ (Common)
$∴ Δ A O B ≅ Δ C O B$ (By SSS congruency)
$∴ ∠ A O B = ∠ C O B$ (By CPCT) --------- (3)
However, $∠ A O B + ∠ C O B = 180^{\circ}$ (Linear pair)
$2 ∠ A O B = 180^{\circ}$ [From equation (3)]
$∠ A O B = 90^{\circ}$ ------------- (4)
Hence, from equation (1), (2) and (4), we see that the diagonals of a square are equal and bisect each other at right angles

|

Updated on:21/07/2023

Class 9 MATHS QUADRILATERALS

Topper's Solved these Questions

Similar Questions

NCERT ENGLISH-QUADRILATERALS-Exercise 8.2

Home
Ask Doubt
Profile