Show that the diagonals of a rhombus are perpendicular to each other
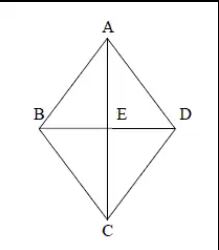
Given: ABCD is a rhombus; AC and BD intersect at E.
To prove: AC⊥BD
In a rhombus, ABCD
AC and BD intersect each Other at E (Given)
In ΔABE and ΔADE
AB=AD (sides of a rhombus)
BE=DE (Diagonals bisect each other)
AE common
∴△ABE=△ADE
⸫AEB+AED (CPCT)
∠AEB+∠AED=180∘
(Linear pair)
⇒AEB=AED=180∘2
=90∘
Hence, AC and BD are perpendicular to each other.
Topper's Solved these Questions
- QUADRILATERALSBook:NCERT ENGLISHChapter:QUADRILATERALSExercise:Exercise 8.2
Explore 7 Videos
- QUADRILATERALSBook:NCERT ENGLISHChapter:QUADRILATERALSExercise:Exercise 8.2
Explore 7 Videos
- PROBABILITYBook:NCERT ENGLISHChapter:PROBABILITYExercise:SOLVED EXAMPLES
Explore 10 Videos
- STATISTICSBook:NCERT ENGLISHChapter:STATISTICSExercise:Exercise 14.2
Explore 9 Videos
Similar Questions
Using analytical geometry, prove that the diagonals of a rhombus are perpendicular to each other.
View SolutionUsing analytical geometry, prove that the diagonals of a rhombus are perpendicular to each other.
View SolutionDiagonals of a rhombus are equal.
View SolutionStatement-l: If the diagonals of the quadrilateral formed by the lines px+gy+r=0,p'x+gy+r'=0,p'x+q'y+r'=0, are at right angles, then p2+q2=p2+q2. Statement-2: Diagonals of a rhombus are bisected and perpendicular to each other.
View SolutionIn a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIf ∣∣→a+→b∣∣=∣∣→a−→b∣∣,(→a,→b≠→0) show that the vectors →aand→b are perpendicular to each other.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a rhombus bisect each other at right angles.
View Solution
