Question

Show that if the diagonals of a quadrilateral are equal and bisect each
other at right angle, then it is a square.

Explanation

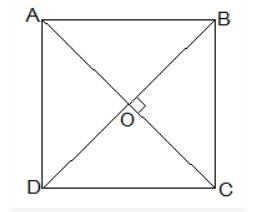
From `ΔAOB` and `ΔCOD`,


`AO = CO` (Diagonals bisect each other)


`∠AOB = ∠COD` (Vertically opposite)


`OB = OD` (Diagonals bisect each other)


`ΔAOB ≅ ΔCOD` [SAS congruency]


Thus,


`AB = CD` [CPCT] — (i)


also,


`∠OAB = ∠OCD` (Alternate interior angles)


`⇒ AB || CD`



Now,


In `ΔAOD` and `ΔCOD`,


`AO = CO` (Diagonals bisect each other)


`∠AOD = ∠COD` (Vertically opposite)


`OD = OD` (Common)


`ΔAOD ≅ ΔCOD` [SAS congruency]


Thus,


`AD = CD` [CPCT] — (ii)


also,

`AD = BC` and `AD = CD`



`⇒ AD = BC = CD = AB` — (ii)


also, `∠ADC = ∠BCD` [CPCT]


and `∠ADC+∠BCD = 180^@` (co-interior angles)


`⇒ 2∠ADC = 180^@`


`⇒∠ADC = 90^@` — (iii)


One of the interior angles is right angle.


Thus, from (i), (ii), and (iii) given quadrilateral ABCD is a square.

Hence Proved.